Advertisements
Advertisements
Question
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
Solution
Let the points be A(a, 2 – 2a), B(– a + 1, 2a) C(– 4 – a, 6 – 2a).
Since the given points are collinear.
Area of a ∆ = 0
`1/2[(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]` = 0

`1/2[((2"a"^2 + (- "a" + 1)(6 - 2"a") + (-4 - "a")(2 - 2"a"))), (-((- "a" + 1)(2 - 2"a") + 2"a"(-4 - "a") + (6 - 2"a")"a"))]` = 0
`1/2[((2"a"^2 - 6"a" + 2"a"^2 + 6 - 2"a" - 8 + 8"a" - 2"a" + 2"a"^2)-), ((-2"a" + 2"a"^2 + 2 - 2"a" - 8"a" - 2"a"^2 + 6"a" - 2"a"^2))]` = 0
`1/2[6"a"^2 - 10"a" + 8"a" - 2 - (2"a"^2 - 4"a"^2 - 12"a" + 6"a" + 2)]` = 0
6a2 – 2a – 2 – (– 2a2 – 6a + 2) = 0
6a2 – 2a – 2 + 2a2 + 6a – 2 = 0
8a2 + 4a – 4 = 0 ...(Divided by 4)
2a2 + a – 1 = 0
2a2 + 2a – a – 1 = 0
2a (a + 1) – 1 (a + 1) = 0
(a + 1) (2a – 1) = 0
a + 1 = 0 or 2a – 1 = 0
a = – 1 or 2a = 1 ⇒ a = `1/2`
The value of a = – 1 or `1/2`
APPEARS IN
RELATED QUESTIONS
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
Trapezium given below; find its area.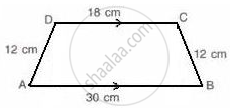
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
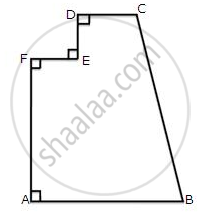
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
Find the diagonal of a quadrilateral whose area is 756cm2 and the perpendicular from the opposite vertices are 17cm and 19cm.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
