Advertisements
Advertisements
Question
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Solution
(i) The breadth of the verandah = x
Length of the verandah = x + 3
According to the question
2( x + ( x + 3 )) = x ( x + 3)
4x + 6 = x2 + 3x
x2 - x - 6 = 0
(ii) From the above equation
x2 - x - 6 = 0
( x - 3 ) ( x + 2 ) = 0
x = 3
Hence breadth = 3m
Length = 3 + 3 = 6m
APPEARS IN
RELATED QUESTIONS
The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
Trapezium given below; find its area.
The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.
Calculate the area of the figure given below: which is not drawn scale.
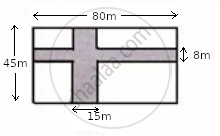
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
The rate for a 1.20 m wide carpet is Rs. 40 per meter; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 wide, is at Rs. 25. Per meter.
Using the information in the following figure, find its area.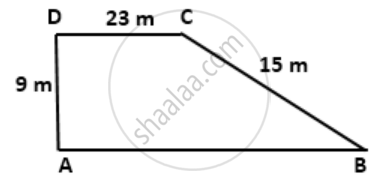
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
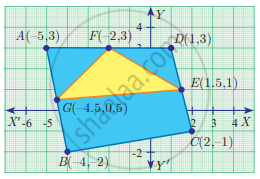
Find the area of quadrilateral BCEG