Advertisements
Advertisements
प्रश्न
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
Advertisements
उत्तर
Consider the figure:
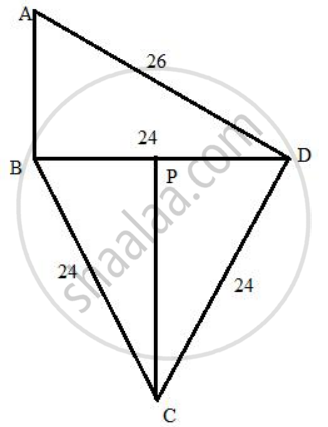
From the right triangle ABD we have
AB = `sqrt(26^2 - 24^2)`
= `2sqrt(13^2 - 12^2)`
= 2 × 5
= 10
The area of right triangle ABC will be
ΔABD = `1/2("AB")("BD")`
= `1/2``(10) (24)`
= 120
Again from the equilateral triangle BCD, we have CP ⊥ BD
PC = `sqrt(24^2 - 12^2)`
= `12sqrt(2^2 - 1^2)`
= `12sqrt(3)`
Therefore, the area of the triangle BCD will be
ΔBCD = `1/2 ("BD")( "PC" )`
= `1/2 (24) (12sqrt3)`
= `144sqrt3`
Hence, the area of the quadrilateral will be
ΔABD + ΔBCD
= 120 + `144sqrt3`
= 369.41 cm2
APPEARS IN
संबंधित प्रश्न
The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.
Trapezium given below; find its area.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
A floor that measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered?
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.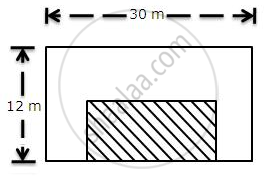
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
