Advertisements
Advertisements
Question
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
Advertisements
Solution
Consider the figure:
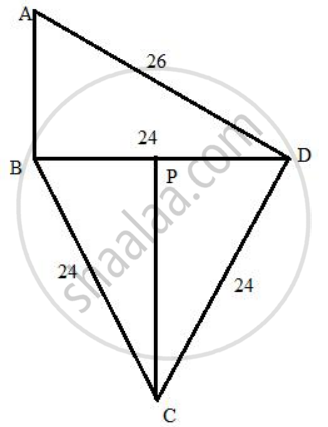
From the right triangle ABD we have
AB = `sqrt(26^2 - 24^2)`
= `2sqrt(13^2 - 12^2)`
= 2 × 5
= 10
The area of right triangle ABC will be
ΔABD = `1/2("AB")("BD")`
= `1/2``(10) (24)`
= 120
Again from the equilateral triangle BCD, we have CP ⊥ BD
PC = `sqrt(24^2 - 12^2)`
= `12sqrt(2^2 - 1^2)`
= `12sqrt(3)`
Therefore, the area of the triangle BCD will be
ΔBCD = `1/2 ("BD")( "PC" )`
= `1/2 (24) (12sqrt3)`
= `144sqrt3`
Hence, the area of the quadrilateral will be
ΔABD + ΔBCD
= 120 + `144sqrt3`
= 369.41 cm2
APPEARS IN
RELATED QUESTIONS
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
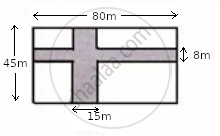
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
In the following, find the value of ‘a’ for which the given points are collinear
(a, 2 – 2a), (– a + 1, 2a) and (– 4 – a, 6 – 2a)
When proving that a quadrilateral is a parallelogram by using slopes you must find
