Advertisements
Advertisements
प्रश्न
A thin metal iron-sheet is rhombus in shape, with each side 10 m. If one of its diagonals is 16 m, find the cost of painting both sides at the rate of ₹ 6 per m2. Also, find the distance between the opposite sides of this rhombus.
उत्तर
Side of rhombus-shaped iron sheet = 10 m and one diagonals (AC) = 16 m
Join BD diagonal which bisects AC at O
The diagonals of a rhombus bisect each other at the right angle
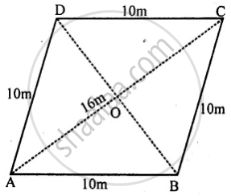
∴ AO = OC = `16/2` = 8m.
Now in right ΔAOB
AB2 = AO2 + BO2 ⇒ (10)2 = (8)2 + BO2
⇒ 100 = 64 + BO2 ⇒ BO2 = 100 - 64 = 36
= (6)2
∴ BO = 6 m
∴ BD = 2 × BO = 2 × 6 = 12 m
Now, the area of rhombus = `(d_1 xx d_2)/2`
= `(16 xx 12)/2 = 96 "m"^2`
Rate of painting = ₹ 6 per m2
∴ The total cost of painting both sides,
= `2 xx 96 xx 6 = ₹ 1152`
Distance between two opposite sides,
= `"Area"/"Base" = 96/10 = 9.6 "m"`
APPEARS IN
संबंधित प्रश्न
Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.
Each side of a rhombus is 18 cm. If the distance between two parallel sides is 12 cm, find its area.
The perimeter of a rhombus is 40 cm. If one diagonal is 16 cm; find:
- It's other diagonal
- area
Find the area of a rhombus whose diagonals are of lengths 10 cm and 8.2 cm.
Find the area of rhombus PQRS shown in the following figure.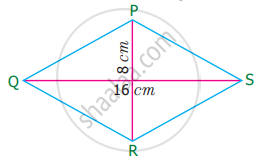
Find the area of rhombus PQRS shown in the following figure.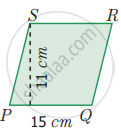
The area of the rhombus is 128 sq.cm and the length of one diagonal is 32 cm. The length of the other diagonal is
One of the diagonals of a rhombus is thrice as the other. If the sum of the length of the diagonals is 24 cm, then find the area of the rhombus.
The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5 m, 3 m, and 350 cm respectively. Find the cost of plastering at the rate of Rs 8 per m2.
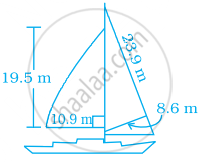
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area sail of the sailboats to the nearest tenth.