Advertisements
Advertisements
Question
A thin metal iron-sheet is rhombus in shape, with each side 10 m. If one of its diagonals is 16 m, find the cost of painting both sides at the rate of ₹ 6 per m2. Also, find the distance between the opposite sides of this rhombus.
Advertisements
Solution
Side of rhombus-shaped iron sheet = 10 m and one diagonals (AC) = 16 m
Join BD diagonal which bisects AC at O
The diagonals of a rhombus bisect each other at the right angle
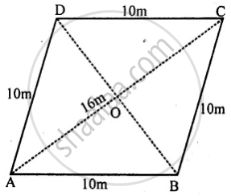
∴ AO = OC = `16/2` = 8m.
Now in right ΔAOB
AB2 = AO2 + BO2 ⇒ (10)2 = (8)2 + BO2
⇒ 100 = 64 + BO2 ⇒ BO2 = 100 - 64 = 36
= (6)2
∴ BO = 6 m
∴ BD = 2 × BO = 2 × 6 = 12 m
Now, the area of rhombus = `(d_1 xx d_2)/2`
= `(16 xx 12)/2 = 96 "m"^2`
Rate of painting = ₹ 6 per m2
∴ The total cost of painting both sides,
= `2 xx 96 xx 6 = ₹ 1152`
Distance between two opposite sides,
= `"Area"/"Base" = 96/10 = 9.6 "m"`
APPEARS IN
RELATED QUESTIONS
The perimeter of a rhombus is 40 cm. If one diagonal is 16 cm; find:
- It's other diagonal
- area
Find the area of rhombus PQRS shown in the following figure.
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 26 m | 468 sq.m |
The area of the rhombus with side 4 cm and height 3 cm is
The area of the rhombus when both diagonals measuring 8 cm is
The angle between the diagonals of a rhombus is
One of the diagonals of a rhombus is thrice as the other. If the sum of the length of the diagonals is 24 cm, then find the area of the rhombus.
A man has to build a rhombus shaped swimming pool. One of the diagonal is 13 m and the other is twice the first one. Then find the area of the swimming pool and also find the cost of cementing the floor at the rate of ₹ 15 per sq.cm
If the diagonals of a rhombus get doubled, then the area of the rhombus becomes ______ its original area.
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of sail of the sailboats to the nearest tenth.
