Advertisements
Advertisements
प्रश्न
A thin metal iron-sheet is rhombus in shape, with each side 10 m. If one of its diagonals is 16 m, find the cost of painting both sides at the rate of ₹ 6 per m2. Also, find the distance between the opposite sides of this rhombus.
उत्तर
Side of rhombus-shaped iron sheet = 10 m and one diagonals (AC) = 16 m
Join BD diagonal which bisects AC at O
The diagonals of a rhombus bisect each other at the right angle
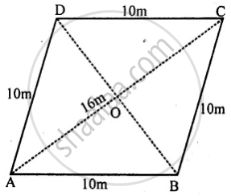
∴ AO = OC = `16/2` = 8m.
Now in right ΔAOB
AB2 = AO2 + BO2 ⇒ (10)2 = (8)2 + BO2
⇒ 100 = 64 + BO2 ⇒ BO2 = 100 - 64 = 36
= (6)2
∴ BO = 6 m
∴ BD = 2 × BO = 2 × 6 = 12 m
Now, the area of rhombus = `(d_1 xx d_2)/2`
= `(16 xx 12)/2 = 96 "m"^2`
Rate of painting = ₹ 6 per m2
∴ The total cost of painting both sides,
= `2 xx 96 xx 6 = ₹ 1152`
Distance between two opposite sides,
= `"Area"/"Base" = 96/10 = 9.6 "m"`
APPEARS IN
संबंधित प्रश्न
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
The diagonals of a rhombus are 18 cm and 24 cm. Find:
(i) its area ;
(ii) length of its sides.
(iii) its perimeter
The area of a rhombus is equal to the area of a triangle. If the base ∆ is 24 cm, its corresponding altitude is 16 cm and one of the diagonals of the rhombus is 19.2 cm. Find its other diagonal.
Find the area of a rhombus whose base is 14 cm and height is 9 cm.
The area of the rhombus is 128 sq.cm and the length of one diagonal is 32 cm. The length of the other diagonal is
A man has to build a rhombus shaped swimming pool. One of the diagonal is 13 m and the other is twice the first one. Then find the area of the swimming pool and also find the cost of cementing the floor at the rate of ₹ 15 per sq.cm
The figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is ______.

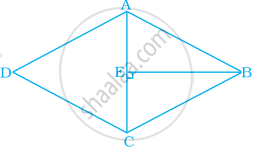
What is the area of the rhombus ABCD below if AC = 6 cm and BE = 4 cm?
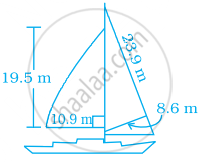
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area sail of the sailboats to the nearest tenth.