Advertisements
Advertisements
प्रश्न
The length of the diagonals of a rhombus is in ratio 4 : 3. If its area is 384 cm2, find its side.
उत्तर
Let the lengths of the diagonals of a rhombus are 4x, 3x.
∴ Area of the rhombus = `1/2 xx ("Product of its diagonals")`
= `1/2 (4x xx 3x) = 384` (given)
⇒ `6x^2 = 384 ⇒ x^2 = 64`
⇒ x = 8 cm
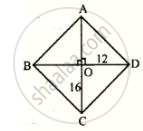
∴ Diagonals are `4 xx 8 = 32` cm and `3(8) = 24` cm.
∴ OC = 16 cm and OD = 12 cm
∴ Side DC = `sqrt("OC"^2 + "OD"^2)`
∴ Side DC = `sqrt(16^2 + 12^2)` [By Pythagoras Theorem in ΔDOC]
= `sqrt(256 + 144) = sqrt(400) = 20` cm
Hence , side of the rhombus = 20 cm.
APPEARS IN
संबंधित प्रश्न
The perimeter of a rhombus is 40 cm. If one diagonal is 16 cm; find:
- It's other diagonal
- area
A thin metal iron-sheet is rhombus in shape, with each side 10 m. If one of its diagonals is 16 m, find the cost of painting both sides at the rate of ₹ 6 per m2. Also, find the distance between the opposite sides of this rhombus.
Find the area of rhombus PQRS shown in the following figure.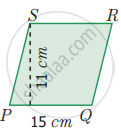
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 12 mm | 180 sq.mm |
The area of the rhombus when both diagonals measuring 8 cm is
The area of the rhombus is 128 sq.cm and the length of one diagonal is 32 cm. The length of the other diagonal is
The angle between the diagonals of a rhombus is
The area of a rectangular field is 48 m2 and one of its sides is 6 m. How long will a lady take to cross the field diagonally at the rate of 20 m/minute?
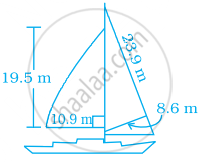
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area sail of the sailboats to the nearest tenth.