Advertisements
Advertisements
प्रश्न
The area of a rhombus is equal to the area of a triangle. If the base ∆ is 24 cm, its corresponding altitude is 16 cm and one of the diagonals of the rhombus is 19.2 cm. Find its other diagonal.
उत्तर
Area of a rhombus = Area of a triangle Base of triangle = 24 cm and altitude = 16 cm
∴ Area = `1/2 "base" xx "altitude"`
= `1/2 xx 24 xx 16 = 192` cm2
∴ Area of rhombus = 192 cm2
one diagonal = 19.2 cm
second diagonal = `("Area" xx 2)/"one diagonal"`
= `(192 xx 2)/19.2 = (192 xx 10 xx 2)/192 = 20` cm
APPEARS IN
संबंधित प्रश्न
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq cm, find its perimeter.
Find the area of rhombus PQRS shown in the following figure.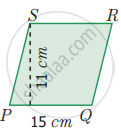
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 26 m | 468 sq.m |
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 12 mm | 180 sq.mm |
A sweet is in the shape of rhombus whose diagonals are given as 4 cm and 5 cm. The surface of the sweet should be covered by an aluminum foil. Find the cost of aluminum foil used for 400 such sweets at the rate of ₹ 7 per 100 sq.cm
The angle between the diagonals of a rhombus is
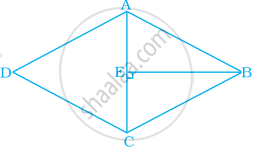
What is the area of the rhombus ABCD below if AC = 6 cm and BE = 4 cm?
The area of a rectangular field is 48 m2 and one of its sides is 6 m. How long will a lady take to cross the field diagonally at the rate of 20 m/minute?
The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5 m, 3 m, and 350 cm respectively. Find the cost of plastering at the rate of Rs 8 per m2.
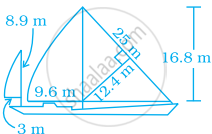
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of sail of the sailboats to the nearest tenth.