Advertisements
Advertisements
Question
The area of a rhombus is equal to the area of a triangle. If the base ∆ is 24 cm, its corresponding altitude is 16 cm and one of the diagonals of the rhombus is 19.2 cm. Find its other diagonal.
Solution
Area of a rhombus = Area of a triangle Base of triangle = 24 cm and altitude = 16 cm
∴ Area = `1/2 "base" xx "altitude"`
= `1/2 xx 24 xx 16 = 192` cm2
∴ Area of rhombus = 192 cm2
one diagonal = 19.2 cm
second diagonal = `("Area" xx 2)/"one diagonal"`
= `(192 xx 2)/19.2 = (192 xx 10 xx 2)/192 = 20` cm
APPEARS IN
RELATED QUESTIONS
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
The perimeter of a rhombus is 40 cm. If one diagonal is 16 cm; find:
- It's other diagonal
- area
A thin metal iron-sheet is rhombus in shape, with each side 10 m. If one of its diagonals is 16 m, find the cost of painting both sides at the rate of ₹ 6 per m2. Also, find the distance between the opposite sides of this rhombus.
Find the area of rhombus PQRS shown in the following figure.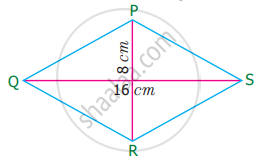
Find the area of rhombus PQRS shown in the following figure.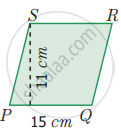
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 26 m | 468 sq.m |
The area of the rhombus when both diagonals measuring 8 cm is
The angle between the diagonals of a rhombus is
The area of the rhombus is 576 sq.cm and the length of one of its diagonal is half of the length of the other diagonal then find the length of the diagonal
Area of a rhombus = `1/2` product of ______.
