Advertisements
Advertisements
Question
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 26 m | 468 sq.m |
Solution
Given diagonal d1 = 26 m
Area of the rhombus = 468 sq.m
`1/2` (d1 × d2) = 468
`1/2` (26 × d2) = 468
(26 × d2) = 468 × 2
d2 = `(468 xx 2)/26`
d2 = 36 m
Tabulating the results we have
| Diagonal (d1) | Diagonal (d2) | Area |
| 26 m | 36 m | 468 sq.m |
APPEARS IN
RELATED QUESTIONS
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq cm, find its perimeter.
The length of the diagonals of a rhombus is in ratio 4 : 3. If its area is 384 cm2, find its side.
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 12 mm | 180 sq.mm |
A sweet is in the shape of rhombus whose diagonals are given as 4 cm and 5 cm. The surface of the sweet should be covered by an aluminum foil. Find the cost of aluminum foil used for 400 such sweets at the rate of ₹ 7 per 100 sq.cm
The area of the rhombus is 576 sq.cm and the length of one of its diagonal is half of the length of the other diagonal then find the length of the diagonal
One of the diagonals of a rhombus is thrice as the other. If the sum of the length of the diagonals is 24 cm, then find the area of the rhombus.
Area of a quadrilateral ABCD is 20 cm2 and perpendiculars on BD from opposite vertices are 1 cm and 1.5 cm. The length of BD is ______.
If the diagonals of a rhombus get doubled, then the area of the rhombus becomes ______ its original area.
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area sail of the sailboats to the nearest tenth.
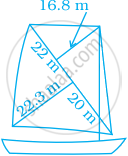
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of sail of the sailboats to the nearest tenth.