Advertisements
Advertisements
Question
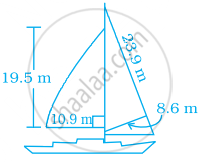
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of sail of the sailboats to the nearest tenth.
Solution
In sailboat,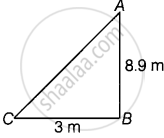
Area of triangle = `1/2` × Base × Height
In ΔABC, AB = 8.9 m and BC = 3 m.
Area of ΔABC = `1/2 xx BC xx AB`
= `1/2 xx 8.9 xx 3`
= `26.7/2`
= 13.35 m2
In another triangular part,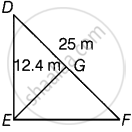
Area of ΔDEF = `1/2 xx DF xx EG`
= `1/2 xx 25 xx 12.4`
= 155 m2
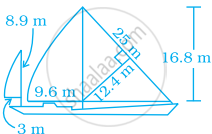
In another triangular part,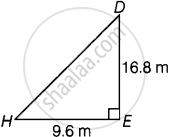
Area of ΔDEH = `1/2 xx DE xx EH`
= `1/2 xx 9.6 xx 16.8`
= 80.64 m2
∴ Area of sailboat = 155 + 80.64 = 235.64 m2
APPEARS IN
RELATED QUESTIONS
Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.
The length of the diagonals of a rhombus is in ratio 4 : 3. If its area is 384 cm2, find its side.
Find the area of a rhombus whose diagonals are of lengths 10 cm and 8.2 cm.
Find the area of a rhombus whose base is 14 cm and height is 9 cm.
Find the missing value.
| Diagonal (d1) | Diagonal (d2) | Area |
| 19 cm | 16 cm |
The height of the rhombus whose area 96 sq.m and side 24 m is
Area of a quadrilateral ABCD is 20 cm2 and perpendiculars on BD from opposite vertices are 1 cm and 1.5 cm. The length of BD is ______.
The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5 m, 3 m, and 350 cm respectively. Find the cost of plastering at the rate of Rs 8 per m2.
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area sail of the sailboats to the nearest tenth.