Advertisements
Advertisements
Question
Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area sail of the sailboats to the nearest tenth.
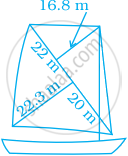
Solution
In the sailboat,
Area of a triangle = `1/2` x Base × Height
In ΔABC, AC = Base = 22 + 20 = 42 m
BD = Height = 23.3 m
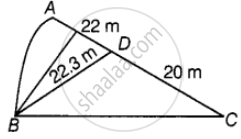
∴ Area of ΔABC = `1/2 xx 42 xx 22.3`
= `936.6/2`
= 468.3 m2
In another triangular part,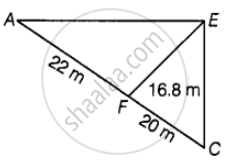
In ΔACE, EF = Height = 16.8 m
AC = Base = 22 + 20 = 42 m
∴ Area of ΔACE = `1/2 xx 42 xx 16.8`
= `705.6/2`
= 352.8 m2
∴ Area of sailboat = 468.3 + 352.8 = 821.1 m2
APPEARS IN
RELATED QUESTIONS
Each side of a rhombus is 18 cm. If the distance between two parallel sides is 12 cm, find its area.
The area of a rhombus is equal to the area of a triangle. If the base ∆ is 24 cm, its corresponding altitude is 16 cm and one of the diagonals of the rhombus is 19.2 cm. Find its other diagonal.
Find the area of a rhombus whose diagonals are of lengths 10 cm and 8.2 cm.
Find the area of rhombus PQRS shown in the following figure.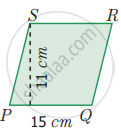
The area of the rhombus when both diagonals measuring 8 cm is
One of the diagonals of a rhombus is thrice as the other. If the sum of the length of the diagonals is 24 cm, then find the area of the rhombus.
A man has to build a rhombus shaped swimming pool. One of the diagonal is 13 m and the other is twice the first one. Then find the area of the swimming pool and also find the cost of cementing the floor at the rate of ₹ 15 per sq.cm
Area of a quadrilateral ABCD is 20 cm2 and perpendiculars on BD from opposite vertices are 1 cm and 1.5 cm. The length of BD is ______.
Area of a rhombus = `1/2` product of ______.
The area of a rectangular field is 48 m2 and one of its sides is 6 m. How long will a lady take to cross the field diagonally at the rate of 20 m/minute?
