Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
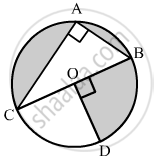
उत्तर
In right triangle ABC
BC2 = AB2 + AC2
= (7)2 + (24)2
= 49 + 576
= 625
∴ BC2 = 625
⇒ BC = 25
Now, ∠COD + ∠BOD = 180° (Linear pair angles)
⇒∠COD = 180° − 90° = 90°
Now, Area of the shaded region = Area of sector having central angle (360° − 90°) − Area of triangle ABC
`=270^circ/360^circpi(BC)^2 - 1/2"AB" × "AC"`
`= 3/4xx3.14xxx(25/2)^2 - 1/2xx7xx24`
= 367.97 × 84
= 283.97 cm2
Hence, the area of shaded region is 283.97 cm2
APPEARS IN
संबंधित प्रश्न
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)

The area of the circle that can be inscribed in a square of side 10 cm is
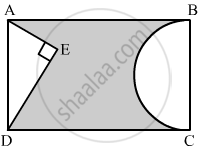
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
A table top is semicircular in shape with diameter 2.8 m. Area of this table top is ______.
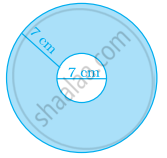
Find the area of the shaded region:
Area of a quadrant of a circle of radius 7 cm is ______.
