Advertisements
Advertisements
प्रश्न
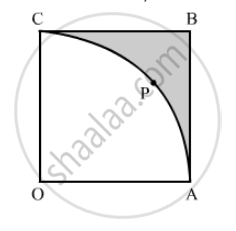
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
उत्तर
Area of shaded region = Area of square OABC − Area of quadrant OAPC
\[ = \left( 7 \right)^2 - \frac{1}{4} \times \frac{22}{7} \times 7 \times 7\]
\[ = 49 - 38 . 5\]
\[ = 10 . 5 {cm}^2\]
Hence, the area of the shaded region is 10.5 cm2
APPEARS IN
संबंधित प्रश्न
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
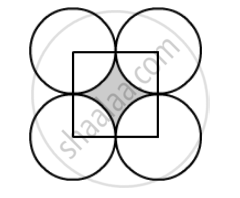
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
If the difference between the circumference and radius of a circle is 37 cm, then its area is
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
The area of a circle is 1386 sq.cm; find its circumference.
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
