Advertisements
Advertisements
प्रश्न
If the difference between the circumference and radius of a circle is 37 cm, then its area is
विकल्प
154 cm2
160 cm2
200 cm2
150 cm2
उत्तर
We have given the difference between circumference and radius of the circle.
Let C be the circumference, r be the radius and A be the area of the circle.
Therefore, from the given condition we have
`C-r=2pir-r`
`∴ 37=2pir-r`
`∴37=r(2pi-1)`
`∴ r=37/((2pi-1))`
Now we will substitute `pi=22/7`
`∴ r= 37/((2xx22/7-1))`
`∴ r=37/((44/7-1))`
`∴ r=37/(((44-7)/7))`
`∴ r=37/((37/7))`
`∴ r=37xx7/37`
`∴ r=7`
Now we will substitute the value of r in`A=pir^2`.
`∴ A=pixx7^2`
Now we will substitute` pi=22/7`
`∴ A=22/7xx7^2`
`∴=22xx7`
`∴ A=154`
Therefore, area of the circle is `154 cm^2`
APPEARS IN
संबंधित प्रश्न
Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
A lawn is in the form of a rectangle whose sides are in the ratio 5 : 3. The area of the lawn is `3375m^2` . Find the cost of fencing the lawn at ₹ 65 per metre.
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
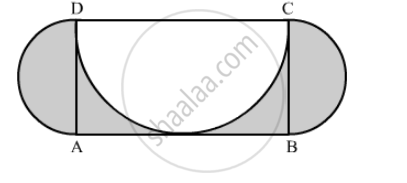
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
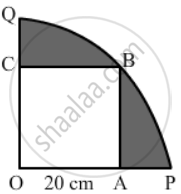
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
The circumference of a circular table is 88 m. Find its area.
The area of the circle is 154 cm2. The radius of the circle is ______.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
