Advertisements
Advertisements
प्रश्न
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
विकल्प
17 \[\sqrt{3}\]units
36 units
72 units
48\[\sqrt{3}\]units
उत्तर
Let the circle of radius r be inscribed in an equilateral triangle of side a.
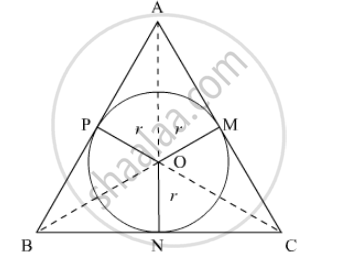
Area of the circle is given as 48π.
`⇒ pir^2=48pi`
`⇒ r^2=48`
`⇒ r=4sqrt3`
Now, it is clear that ON⊥BC. So, ON is the height of ΔOBC corresponding to BC.
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB = 3 × Area of ΔOBC
`sqrt3/4xxa^2=3xx1/2xxBCxxON`
`sqrt3/4xxa^2=3xx1/2xxaxxr`
`sqrt3/4xxa^2=3xx1/2xxaxx4sqrt3`
`a=24`
Thus, perimeter of the equilateral triangle = 3 × 24 units = 72 units
APPEARS IN
संबंधित प्रश्न
A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
In the following figure find the area of the shaded region. (Use π = 3.14)
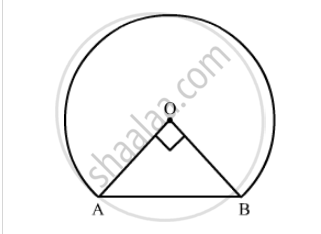
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
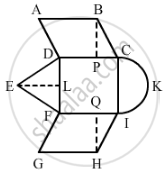
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
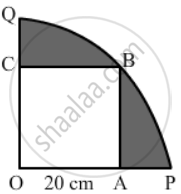
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
The area of a circle is 1386 sq.cm; find its circumference.
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


