Advertisements
Advertisements
प्रश्न
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
पर्याय
17 \[\sqrt{3}\]units
36 units
72 units
48\[\sqrt{3}\]units
उत्तर
Let the circle of radius r be inscribed in an equilateral triangle of side a.
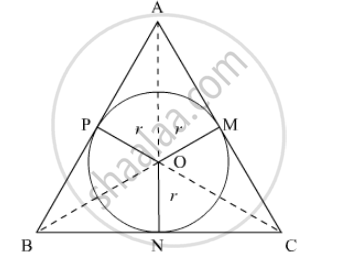
Area of the circle is given as 48π.
`⇒ pir^2=48pi`
`⇒ r^2=48`
`⇒ r=4sqrt3`
Now, it is clear that ON⊥BC. So, ON is the height of ΔOBC corresponding to BC.
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB = 3 × Area of ΔOBC
`sqrt3/4xxa^2=3xx1/2xxBCxxON`
`sqrt3/4xxa^2=3xx1/2xxaxxr`
`sqrt3/4xxa^2=3xx1/2xxaxx4sqrt3`
`a=24`
Thus, perimeter of the equilateral triangle = 3 × 24 units = 72 units
APPEARS IN
संबंधित प्रश्न
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
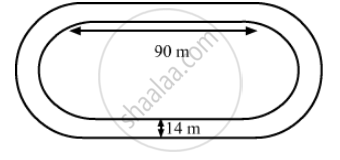
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
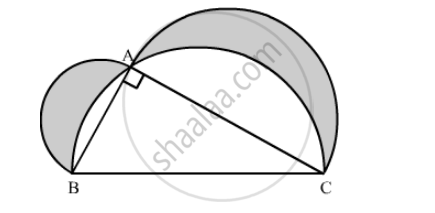
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
If the circumference of a circle increases from 4π to 8π, then its area is
A wire is bent to form a square enclosing an area of 484 cm2. Using the same wire, a circle is formed. Find the area of the circle.
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)" cm"^2`. If the same wire is bent into the form of a circle, what will be the area of the circle?
