Advertisements
Advertisements
Question
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
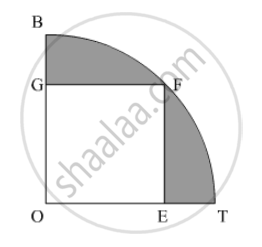
Solution
We have to find the area of the shaded portion. We have, `OE=20cm`and OEFG is a square.
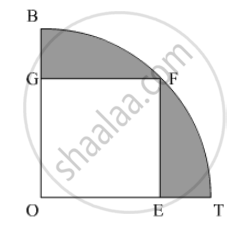
Use Pythagoras theorem to find OF as,
`OF=(sqrt((20)^2+(20)^2))cm`
`= 20sqrt2 cm`
So, radius of the circle,
`OF=20sqrt2 cm`
Therefore area of the shaded region,
`"Area of the shade region=(Area of quadrant of circle)-(Area of square)"`
So,
Area of the shaded region =`(pi(OF)^2)/4-(OE)^2`
`(22/7)((20sqrt2^2)/4)-(20)^2`
=`628-400`
`=228 cm^2`
APPEARS IN
RELATED QUESTIONS
A 36-m-long, 15-m-borad verandah is to be paved with stones, each measuring 6dm by 5 dm. How many stones will be required?
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
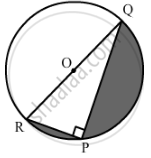
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
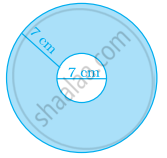
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
Find the area of the shaded region: