Advertisements
Advertisements
Question
An arc subtends an angle of 90° at the centre of the circle of the radius 14 cm. Write the area of minor sector thus formed in terms of π.
Solution
We have given an angle subtended by an arc at the centre of the circle and radius of the circle.
`r=14 cm`
`θ=90°`
Now we will find the area of the minor sector.
Area of the minor sector =`θ/360xxpir^2`
Substituting the values we get,
Area of the minor sector = `90/360xxpixx14^2`.......(1)
Now we will simplify the equation (1) as below,
Area of the minor sector `=1/4xxpixx14^2`
`"Area of the minor sector" =1/4xxpixx14xx14`
`"Area of the minor sector" =pixx7xx7`
Area of the minor sector = `49 pi`
Therefore, area of the minor sector is `49 pi cm^2`
APPEARS IN
RELATED QUESTIONS
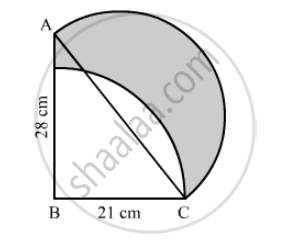
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
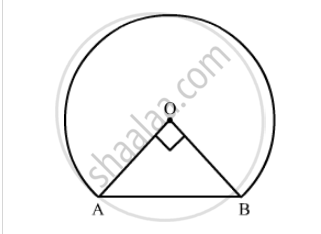
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
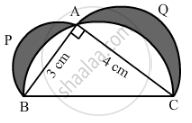
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
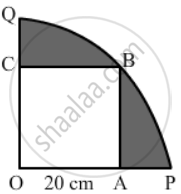
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
The sum of diameters of two circles is 112cm and the sum of their areas is 5236cm2. Find the radii of the two circles.
