Advertisements
Advertisements
Question
The outer circumference of a circular race-track is 528 m . The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre.
`(use pi=22/7). `
Solution
Let the radius of the inner circle and the race track be R m.
Outer circumference of the race track = 528 m
`⇒ 2 pi R=528`
`⇒ R=528/2pi=84 m`
Total radius of the outer circle =` 84-14=70 m`
Area of the circular track = Area of the outer circle − area of inner circle
`= pi(84)^2-pi(70)^2`
`= pi [(84-70)(84+70)]`
`=pi(14)(154)`
`=6776 m^2`
Cost of levelling the track =` 0.5xx6776=Rs 3388`
APPEARS IN
RELATED QUESTIONS
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
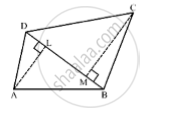
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
A road which is 7 m wide surrounds a circular park whose circumference is 352 m . Find the area of the road .
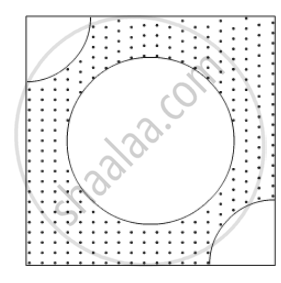
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
A square tank has an area of 1600 cm2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs 12.50 per m2
