Advertisements
Advertisements
प्रश्न
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
उत्तर
Given: Area of triangle `24cm^2`
Let the sides be a and b, where a is the height and b is the base of triangle
`a-b=2cm`
`a=2+b` .............(1)
Area of triangle =`1/2xxbxxh`
⇒`24=1/2xxbxx(2+b)`
⇒`48=b+1/2b^2`
⇒`48=2b+b^2`
⇒`b^2+2b-48=0`
⇒`(b+8)(b-6)=0`
⇒`b=-8 or 6`
Side of a triangle cannot e negative.
Therefore, b=cm
Substituting the value of b=6 cm in equation (1), we get :
`a=2+6=8cm`
Now, `a=8cm, b=6cm`
In the given right triangle we have to find third side. Using the relation
`"(Hyp)"^2="(Oneside)"^2+"(otherside)"^2`
⇒`Hyp^2=8^2+6^2`
⇒`Hyp^2=64+36`
⇒`Hyp^2=100`
⇒`Hyp^2=10 cm`
So, the third side is 10 cm So,
perimeter of the triangle `a+b+c`
=`8+6+10`
=`24cm`
APPEARS IN
संबंधित प्रश्न
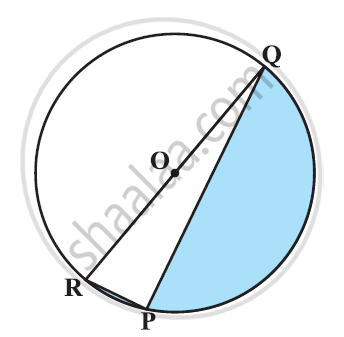
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
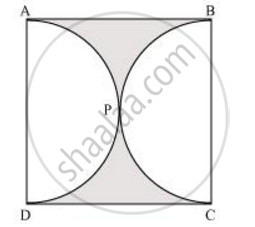
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
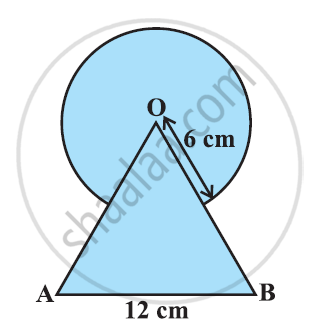
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
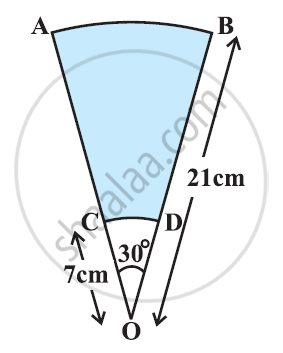
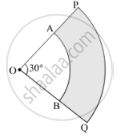
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
Find the area of the shaded region in figure.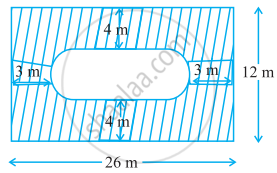
Read the following passage:
Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a hill, which will have adequate space for parking.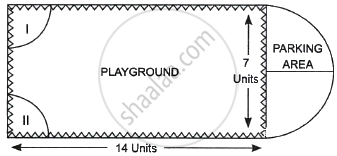 After survey, it was decided to build rectangular playground, with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and 7 units, respectively. There are two quadrants of radius 2 units on one side for special seats. |
Based on the above information, answer the following questions:
- What is the total perimeter of the parking area?
- (a) What is the total area of parking and the two quadrants?
OR
(b) What is the ratio of area of playground to the area of parking area? - Find the cost of fencing the playground and parking area at the rate of ₹ 2 per unit.
