Advertisements
Advertisements
प्रश्न
Find the area of the shaded region in figure.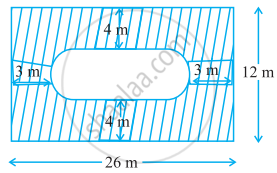
उत्तर
Join GH and FE such that EFGH is the rectangle.
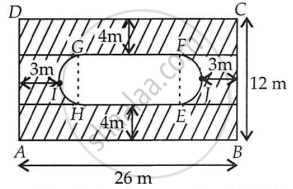
Here, breadth of the rectangle ABCD = BC = 12 m
∴ Breadth of the inner rectangle EFGH = EF
= [12 – (4 + 4)] m
= 4 m
which is equal to the diameter of the semi-circle EJF = 4 m
∴ Radius of semi-circle EJF, (r) = 2 m
Length of inner rectangle EFGH = EH
= [26 – (5 + 5)] m
= 16 m
∴ Area of two semi-circles EJF and HIG
= `2((π"r"^2)/2)`
= `2 xx (π(2)^2)/2 "m"^2`
= 4π m2
Now, area of inner rectangle EFGH
= EH × EF
= (16 × 4) m2
= 64 m2
And area of outer rectangle ABCD
= (26 × 12) m2
= 312 m2
∴ Area of shaded region = Area of outer rectangle – (Area of two semi-circles + Area of inner rectangle)
= [312 – (4π + 64)] m2
= (248 – 4π) m2
APPEARS IN
संबंधित प्रश्न
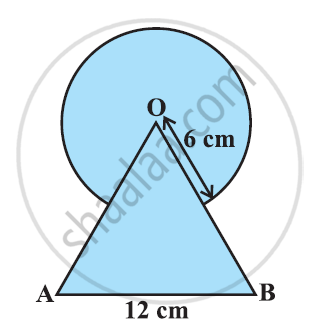
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
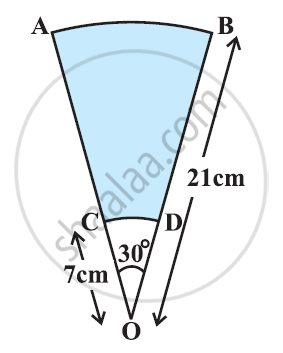
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
Find the areas of the triangle whose sides are 42 cm, 34 cm and 20 cm. Also, find the height corresponding to the longest side.
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
The height of an equilateral triangle is 6 cm. Find its area.
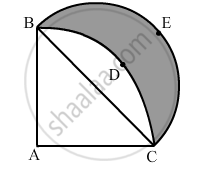
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
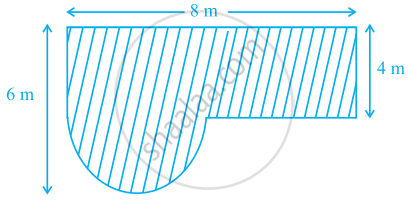
Find the area of the shaded field shown in figure.