Advertisements
Advertisements
प्रश्न
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
उत्तर
Let ABC be the triangle such that A (2, 1), B (4, 3) and C (2, 5) are the vertices of the triangle.
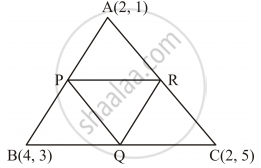
Let P, Q and R be the mid-points of sides AB, BC and CA respectively of ΔABC.
`\text{Coordination of the mid-point of points}(x_1,y_2) and (x_2,y_2)=((x_1+x_2)/2, (y_1+y_2)/2)`
`\text{Coordination of P}`=`((4+2)/2, (3+1)/2)=(3,2)`
`\text{Coordination of Q}`=`((4+2)/2, (3+5)/2)=(3,4)`
`\text{Coordination of Q}`=`((2+2)/2, (5+1)/2)=(2,3)`
The area of the triangle whose vertices are (x1 , y1 ), (x2 , y2 ) and (x3 , y3 ) is given as follows:
`1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
∴Area of ΔPQR
`=1/2[3(4-3)+3(3-2)+2(2-4)]`
`=1/2[3(1)+3(1)+2(-2)]`
`=1/2[3+3-4]`
`=2/2`
`=1 sq.unit`
Thus, the area of the triangle formed by joining the mid-points of the sides of the given triangle
is 1 sq unit.
APPEARS IN
संबंधित प्रश्न
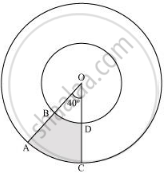
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
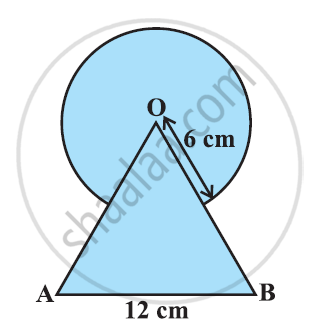
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

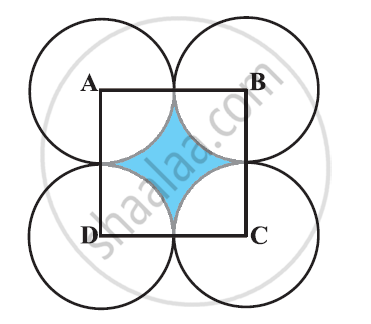
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
If the area of an equilateral triangle is `81sqrt3 cm^2` find its height.
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.


