Advertisements
Advertisements
Question
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
Solution
Let ABC be the triangle such that A (2, 1), B (4, 3) and C (2, 5) are the vertices of the triangle.
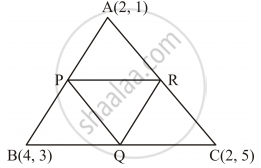
Let P, Q and R be the mid-points of sides AB, BC and CA respectively of ΔABC.
`\text{Coordination of the mid-point of points}(x_1,y_2) and (x_2,y_2)=((x_1+x_2)/2, (y_1+y_2)/2)`
`\text{Coordination of P}`=`((4+2)/2, (3+1)/2)=(3,2)`
`\text{Coordination of Q}`=`((4+2)/2, (3+5)/2)=(3,4)`
`\text{Coordination of Q}`=`((2+2)/2, (5+1)/2)=(2,3)`
The area of the triangle whose vertices are (x1 , y1 ), (x2 , y2 ) and (x3 , y3 ) is given as follows:
`1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
∴Area of ΔPQR
`=1/2[3(4-3)+3(3-2)+2(2-4)]`
`=1/2[3(1)+3(1)+2(-2)]`
`=1/2[3+3-4]`
`=2/2`
`=1 sq.unit`
Thus, the area of the triangle formed by joining the mid-points of the sides of the given triangle
is 1 sq unit.
APPEARS IN
RELATED QUESTIONS
The given figure depicts a racing track whose left and right ends are semicircular.
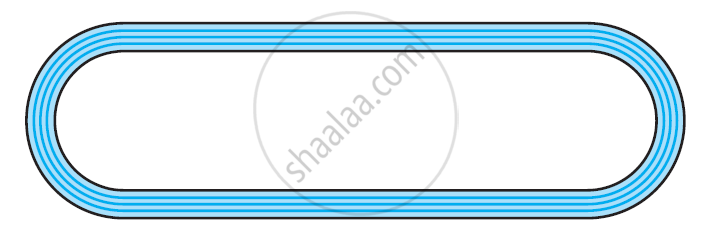
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
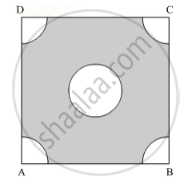
In Figure 4, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14)
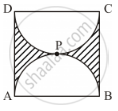
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
Find the area of the shaded region in figure.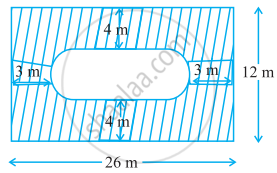
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.


