Advertisements
Advertisements
Question
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
Solution
Let the sides of triangle be a=18 cm, b=24 cm and c=30 cm
Let s be the semi-perimeter of the triangle.
s=`1/2(a+b+c)`
s=`1/2(18+24+30)`
s=`36 cm`
Area of a triangle = `sqrt(s(s-a)(s-b)(s-c))`
=`sqrt(36(36-18)(36-24)(36-30))`
=`sqrt(36xx18xx12xx6)`
=`sqrt(46656)`
=`216 cm^2`
The smallest side is 18 cm long. This is the base.
Now, area of a triangle = `1/2xxbxxh`
⇒ `216=1/2xx18xxh`
⇒ `216=9h`
⇒`216/9=h`
⇒` h=24 cm`
The height corresponding to the smallest side is 24 cm
APPEARS IN
RELATED QUESTIONS
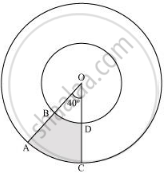
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
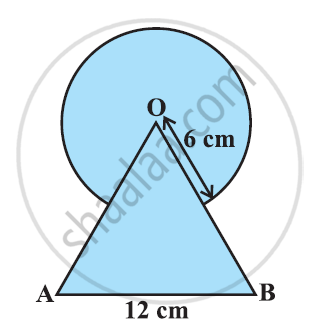
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
If the area of an equilateral triangle is `36sqrt3 cm^2` find its perimeter.
If the area of an equilateral triangle is `81sqrt3 cm^2` find its height.
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
Find the area of the flower bed (with semi-circular ends) shown in figure.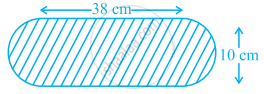
Find the area of the shaded region in figure.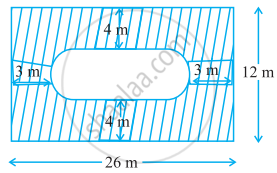
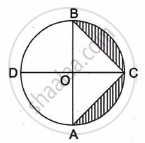
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.