Advertisements
Advertisements
Question
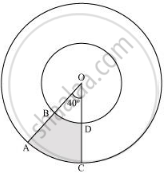
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
Solution
 ]
]
Radius of inner circle = 7 cm
Radius of outer circle = 14 cm
Area of shaded region = Area of sector OAFC − Area of sector OBED
`= 40^@/360^@ xx pi(14)^2 - 40^@/360^@ xx pi(7)^2`
`= 1/9xx22/7xx14xx14-1/9xx22/7xx7xx7`
`= 616/9-154/9=462/9`
`= 154/3 cm^2`
APPEARS IN
RELATED QUESTIONS
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
The height of an equilateral triangle is 6 cm. Find its area.
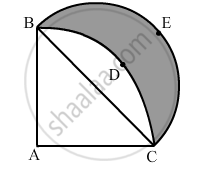
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Find the area of the shaded field shown in figure.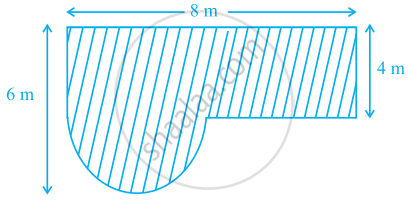
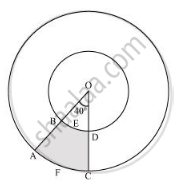
Find the area of the shaded region in figure.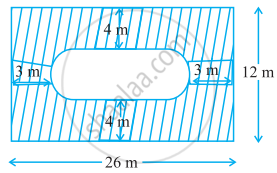
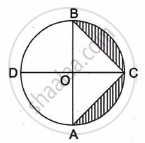
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.