Advertisements
Advertisements
Question
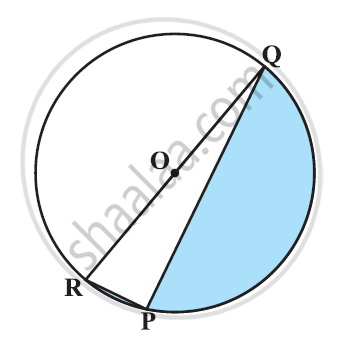
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
Solution
It can be observed that RQ is the diameter of the circle. Therefore, ∠RPQ will be 90º.
By applying Pythagoras theorem in ΔPQR,
RP2 + PQ2 = RQ2
(7)2 + (24)2 = RQ2
`RQ = sqrt625 = 25`
Radius of circle, OR = RQ/2 = 25/2
Since RQ is the diameter of the circle, it divides the circle in two equal parts.
Area of semi circle RPQOR = `1/2 pir^2`
`= 1/2pi(25/2)^2`
`=1/2xx22/7xx625/4`
`=6875/28 cm^2`
Area of ΔPQR = `1/2 xx PQ xxPR`
`= 1/2 xx 24 xx 7`
= 84 cm2
Area of shaded region = Area of semi-circle RPQOR − Area of ΔPQR
= 6875/28 - 84
`= (6875 - 2352)/28`
`= 4523/28 cm^2`
APPEARS IN
RELATED QUESTIONS
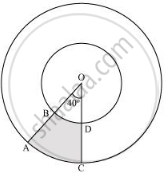
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
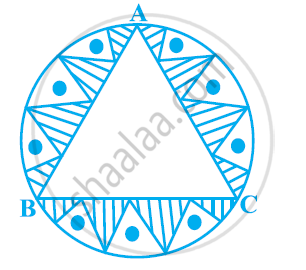
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
The height of an equilateral triangle is 6 cm. Find its area.
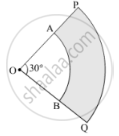
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
Find the area of the shaded field shown in figure.