Advertisements
Advertisements
Question
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

Solution
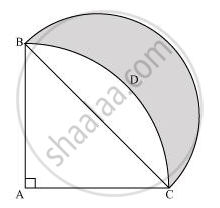
As ABC is a quadrant of the circle, ∠BAC will be of measure 90º.
In ΔABC,
BC2 = AC2 + AB2
= (14)2 + (14)2
BC = 14sqrt2
Radius (r1) of semi-circle drawn on BC = `(14sqrt2)/2 = 7sqrt2 cm`
Area of ΔABC = 1/2 x AB x AC
= 1/2 x 14 x 14
= 98 cm2
Area of sector ABDC = `90^@/360^@ xx pir^2`
`= 1/4 xx 22/7 xx 14 xx 14`
=154 cm2
Area of semi circle drawn of BC = `1/2xxpixxr_1^2 = 1/2 xx 22/7 xx (7sqrt2)^2`
`= 1/2 xx 22/7xx 98 = 154 cm^2`
Area of shaded region = Area of semi- circle - (Area of sector ABDC - Area of ΔABC) = 154 - (154-98)
= 98 cm2
APPEARS IN
RELATED QUESTIONS
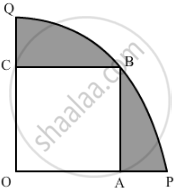
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

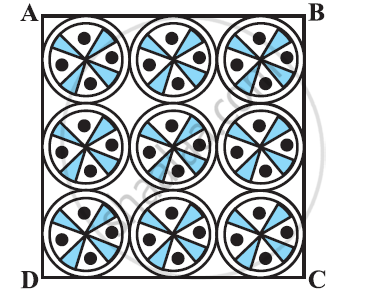
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
Find the areas of the triangle whose sides are 42 cm, 34 cm and 20 cm. Also, find the height corresponding to the longest side.
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
