Advertisements
Advertisements
प्रश्न
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

उत्तर
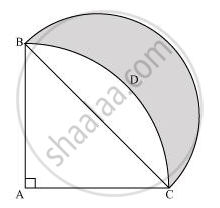
As ABC is a quadrant of the circle, ∠BAC will be of measure 90º.
In ΔABC,
BC2 = AC2 + AB2
= (14)2 + (14)2
BC = 14sqrt2
Radius (r1) of semi-circle drawn on BC = `(14sqrt2)/2 = 7sqrt2 cm`
Area of ΔABC = 1/2 x AB x AC
= 1/2 x 14 x 14
= 98 cm2
Area of sector ABDC = `90^@/360^@ xx pir^2`
`= 1/4 xx 22/7 xx 14 xx 14`
=154 cm2
Area of semi circle drawn of BC = `1/2xxpixxr_1^2 = 1/2 xx 22/7 xx (7sqrt2)^2`
`= 1/2 xx 22/7xx 98 = 154 cm^2`
Area of shaded region = Area of semi- circle - (Area of sector ABDC - Area of ΔABC) = 154 - (154-98)
= 98 cm2
APPEARS IN
संबंधित प्रश्न
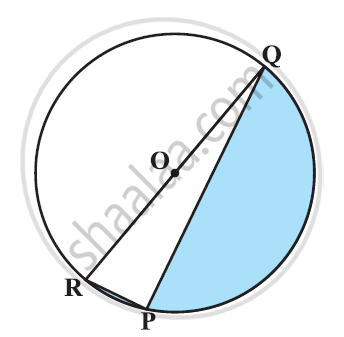
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

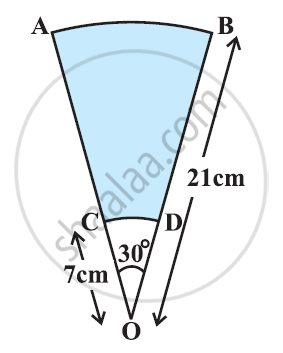
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
If the area of an equilateral triangle is `36sqrt3 cm^2` find its perimeter.
If the area of an equilateral triangle is `81sqrt3 cm^2` find its height.
Find the area of shaded region in Fig. 4, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (Use π = 3.14 and\[\sqrt{3}\] =1.73)
Read the following passage:
Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a hill, which will have adequate space for parking.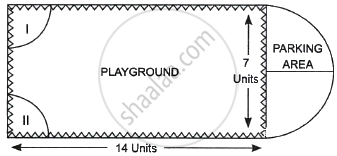 After survey, it was decided to build rectangular playground, with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and 7 units, respectively. There are two quadrants of radius 2 units on one side for special seats. |
Based on the above information, answer the following questions:
- What is the total perimeter of the parking area?
- (a) What is the total area of parking and the two quadrants?
OR
(b) What is the ratio of area of playground to the area of parking area? - Find the cost of fencing the playground and parking area at the rate of ₹ 2 per unit.
