Advertisements
Advertisements
प्रश्न
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

उत्तर
Let the side of the equilateral triangle be a.
Area of equilateral triangle = 17320.5 cm2
sqrt3/4(s)^2 = 17320.5
1.7320/4a^2 = 17320.5
a2 = 4 x 10000
a = 200 cm
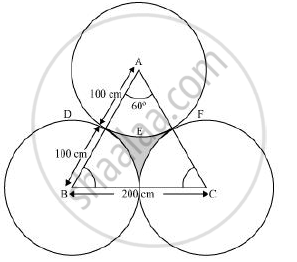
Each sector is of measure 60°.
Area of sector ADEF = `60^@/360^@ xx pixxr^2`
`=1/6xxpixx(100)^2`
`=(3.14xx10000)/6`
`= 15700/3 cm^2`
Area of shaded region = Area of equilateral triangle − 3 × Area of each sector
`= 17320.5 - 3xx 15700/3`
= 17320.5-15700 = 1620.5 cm2
APPEARS IN
संबंधित प्रश्न
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

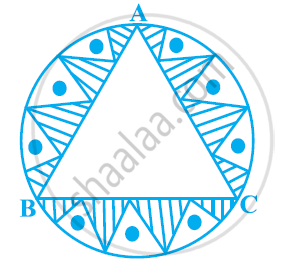
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
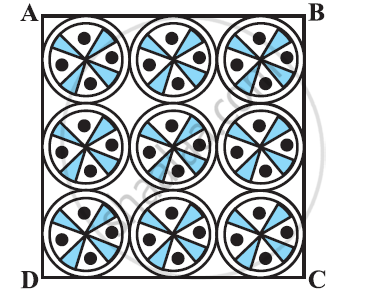
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
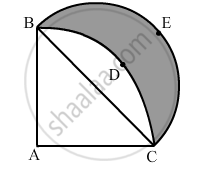
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
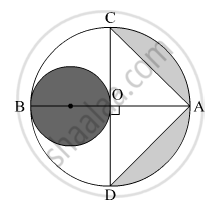
In Fig.5, AB and CD are two diameters of a circle with centre O, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. `[\text{Use}pi=22/7]`
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
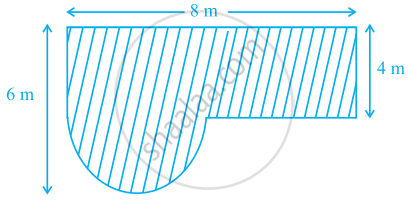
Find the area of the shaded field shown in figure.