Advertisements
Advertisements
प्रश्न
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

उत्तर
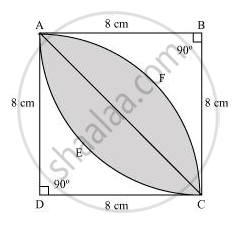
The designed area is the common region between two sectors BAEC and DAFC.
Area of sector BAEC = `90^@/360^@ xx 22/7xx(8)^2`
`=1/4xx22/7xx64`
`=(22xx16)/7 cm^2`
`= 352/7 cm^2`
Area of ΔBAC = `1/2xxBAxxBC`
`= 1/2xx8xx7 = 32 cm^2`
Area of the designed portion = 2 × (Area of segment AEC)
= 2 × (Area of sector BAEC − Area of ΔBAC)
`= 2xx(352/7 - 32) = 2((352-224)/4)`
`= (2xx128)/7`
`= 256/7 cm^2`
APPEARS IN
संबंधित प्रश्न
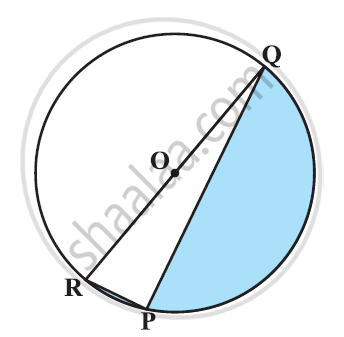
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
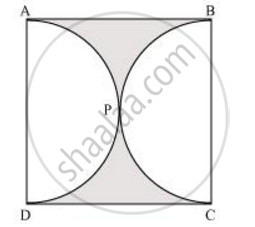
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
If the area of an equilateral triangle is `81sqrt3 cm^2` find its height.
Find the area of shaded region in Fig. 4, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (Use π = 3.14 and\[\sqrt{3}\] =1.73)
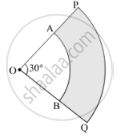
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
Find the area of the flower bed (with semi-circular ends) shown in figure.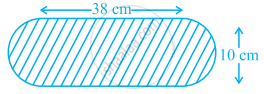
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.