Advertisements
Advertisements
प्रश्न
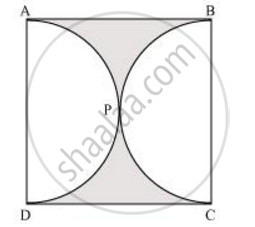
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
उत्तर
It can be observed from the figure that the radius of each semi-circle is 7 cm.
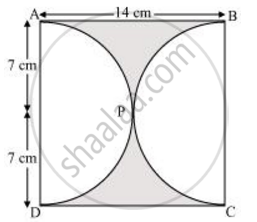
Area of each semi-circle = `1/2 pir^2`
`= 1/2xx22/7xx(7)^2`
= 77 cm2
Area of square ABCD = (Side)2 = (14)2 = 196 cm2
Area of the shaded region
= Area of square ABCD − Area of semi-circle APD − Area of semi-circle BPC
= 196 − 77 − 77 = 196 − 154 = 42 cm2
APPEARS IN
संबंधित प्रश्न
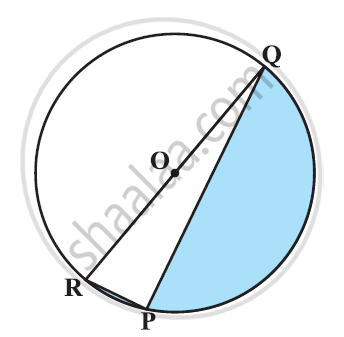
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
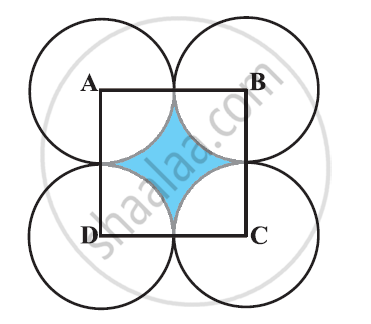
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
The given figure depicts a racing track whose left and right ends are semicircular.
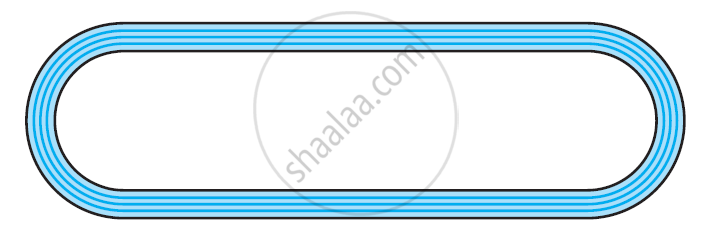
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
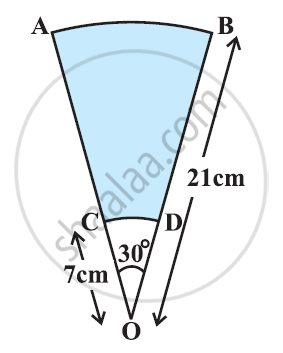
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
