Advertisements
Advertisements
Question
A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
Solution

Dimensions of rectangular park length = 120m
Breadth = 100m
Area of park = l × b
= 120 × 100 = 12000𝑚2.
𝐿𝑒𝑡 𝑟𝑎𝑑𝑖𝑢𝑠 𝑜𝑓 𝑐𝑖𝑟𝑐𝑢𝑙𝑎𝑟 𝑙𝑎𝑤𝑛 𝑏𝑒 𝑟
Area of circular lawn = 𝜋𝑟2
Area of remaining park excluding lawn = (area of park) – (area of circular lawn)
⇒ 8700 = 12000 – 𝜋r2
⇒ 𝜋r2 = 12000 – 8700 = 3300
⇒`22/7× r^2 = 3300`
⇒ `r^2` = 150 × 7 = 1050
⇒ `r = sqrt(1050) = 5sqrt(42)` 𝑚𝑒𝑡𝑟𝑒𝑠
∴ radius of circular lawn = 5`sqrt(42)` metres.
APPEARS IN
RELATED QUESTIONS
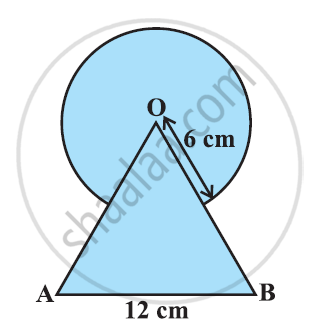
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

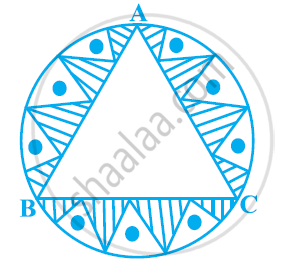
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
If the area of an equilateral triangle is `81sqrt3 cm^2` find its height.
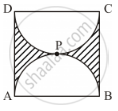
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`