Advertisements
Advertisements
प्रश्न
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
उत्तर
Let the sides of triangle be a=18 cm, b=24 cm and c=30 cm
Let s be the semi-perimeter of the triangle.
s=`1/2(a+b+c)`
s=`1/2(18+24+30)`
s=`36 cm`
Area of a triangle = `sqrt(s(s-a)(s-b)(s-c))`
=`sqrt(36(36-18)(36-24)(36-30))`
=`sqrt(36xx18xx12xx6)`
=`sqrt(46656)`
=`216 cm^2`
The smallest side is 18 cm long. This is the base.
Now, area of a triangle = `1/2xxbxxh`
⇒ `216=1/2xx18xxh`
⇒ `216=9h`
⇒`216/9=h`
⇒` h=24 cm`
The height corresponding to the smallest side is 24 cm
APPEARS IN
संबंधित प्रश्न
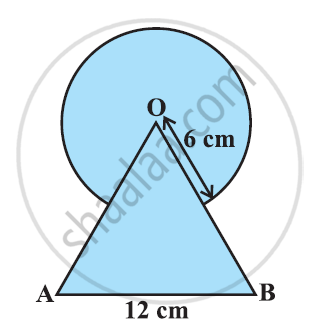
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
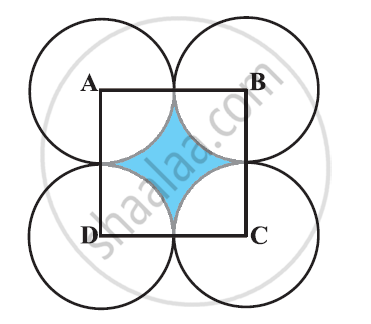
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

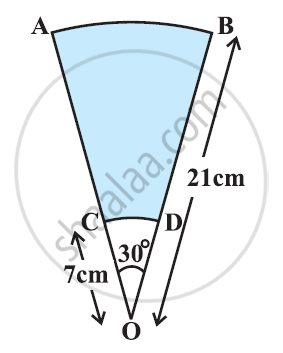
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
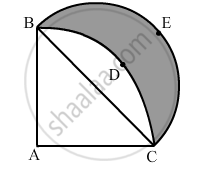
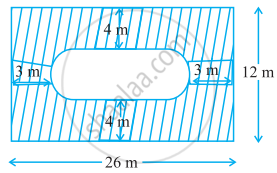
Find the area of the shaded region in figure.