Advertisements
Advertisements
Question
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
Solution
Given: Area of triangle `24cm^2`
Let the sides be a and b, where a is the height and b is the base of triangle
`a-b=2cm`
`a=2+b` .............(1)
Area of triangle =`1/2xxbxxh`
⇒`24=1/2xxbxx(2+b)`
⇒`48=b+1/2b^2`
⇒`48=2b+b^2`
⇒`b^2+2b-48=0`
⇒`(b+8)(b-6)=0`
⇒`b=-8 or 6`
Side of a triangle cannot e negative.
Therefore, b=cm
Substituting the value of b=6 cm in equation (1), we get :
`a=2+6=8cm`
Now, `a=8cm, b=6cm`
In the given right triangle we have to find third side. Using the relation
`"(Hyp)"^2="(Oneside)"^2+"(otherside)"^2`
⇒`Hyp^2=8^2+6^2`
⇒`Hyp^2=64+36`
⇒`Hyp^2=100`
⇒`Hyp^2=10 cm`
So, the third side is 10 cm So,
perimeter of the triangle `a+b+c`
=`8+6+10`
=`24cm`
APPEARS IN
RELATED QUESTIONS
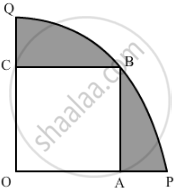
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
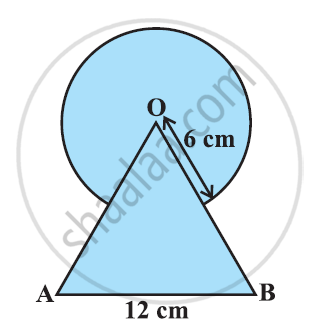
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
The given figure depicts a racing track whose left and right ends are semicircular.
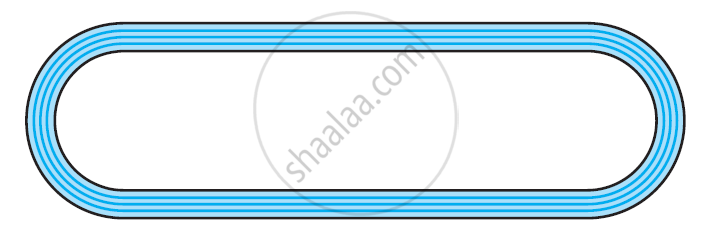
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
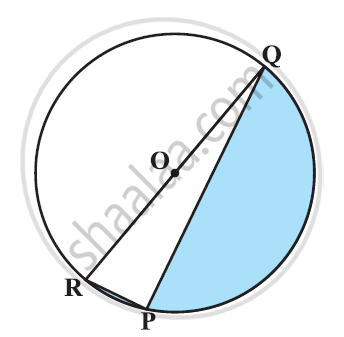
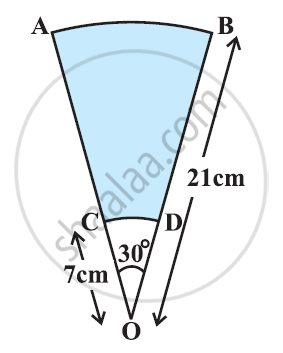
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
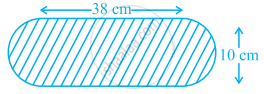
Find the area of the flower bed (with semi-circular ends) shown in figure.