Advertisements
Advertisements
प्रश्न
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.
उत्तर
i. Area of square ABCD = (Side)2,
= (8)2
= 64 cm2
ii. ΔABC, ∠B = 90°
∴ AC2 = AB2 + BC2 = 2AB2
AC = `sqrt(2) "AB"`
Diagonal AC = `8sqrt(2) "cm"`
iii. Area of Sector OPRQO
= `θ/360 πr^2`
= `90^circ/360^circ xx 22/7 xx 4 xx 4 "cm"^2`
[Radius of inscribed circle = `1/2` side of square]
Area of sector OPRQO = `88/7`
= `12 4/7 "cm"^2`
OR
Area of circle = πr2
= `22/7 xx (4)^2`
= `352/7 "cm"^2`
∴ Required Area = `64 - 352/7`
= `(448 - 352)/7`
= `96/7 "cm"^2`
= `13 5/7 "cm"^2`
APPEARS IN
संबंधित प्रश्न
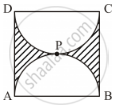
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
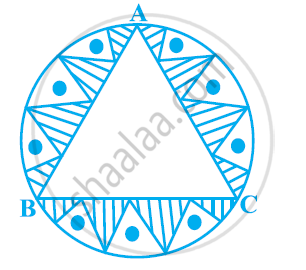
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

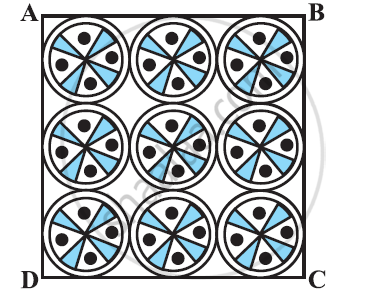
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
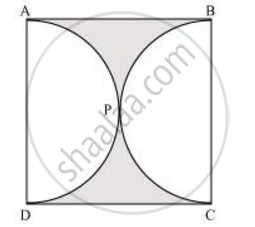
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
If the area of an equilateral triangle is `36sqrt3 cm^2` find its perimeter.
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`