Advertisements
Advertisements
प्रश्न
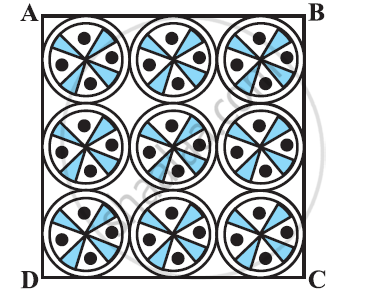
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
उत्तर
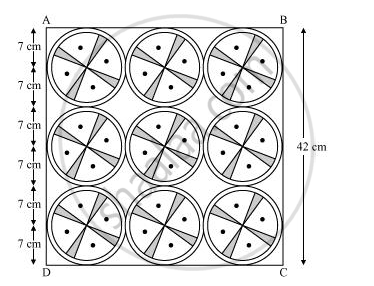
From the figure, it can be observed that the side of the square is 42 cm.
Area of square = (Side)2 = (42)2 = 1764 cm2
Area of each circle = πr2 = `22/7 xx (7)^2 = 154 cm^2`
Area of 9 circles = 9 × 154 = 1386 cm2
Area of the remaining portion of the handkerchief = 1764 − 1386 = 378 cm2
APPEARS IN
संबंधित प्रश्न
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

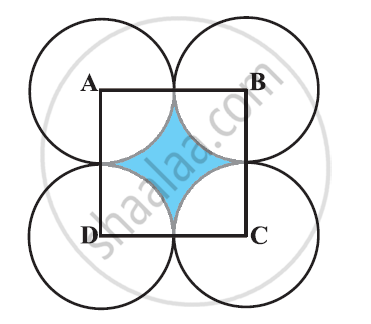
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
The given figure depicts a racing track whose left and right ends are semicircular.
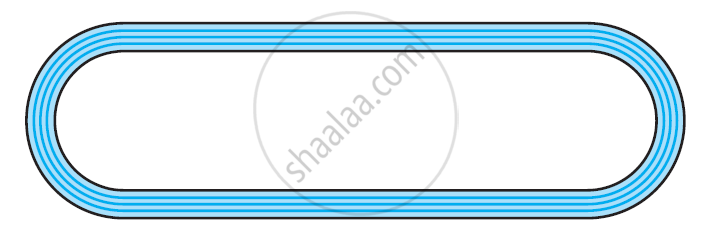
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
The height of an equilateral triangle is 6 cm. Find its area.
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
