Advertisements
Advertisements
प्रश्न
If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
उत्तर
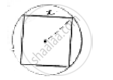
Let side of square be x cms inscribed in a circle.
Radius of circle (r) =`1/2`(𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙 𝑜𝑓 𝑠𝑞𝑢𝑎𝑟𝑒)
`=1/2(sqrt(2x))`
`=x/sqrt(2)`
Area of square = (side)2 = x2
Area of circle = 𝜋r2
`=pi( x/sqrt(2))^2`
`=(pix^2)/2`
`"Area of circle"/"Area of square"=(pi/2x^2)/x^2=pi/2=pi:2`
APPEARS IN
संबंधित प्रश्न
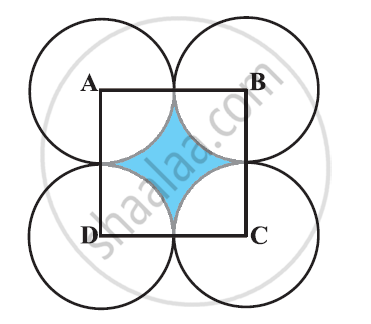
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
The given figure depicts a racing track whose left and right ends are semicircular.
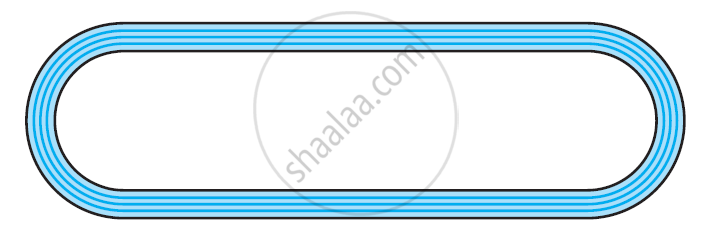
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

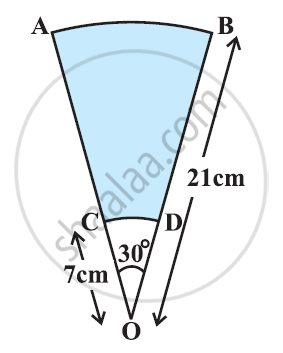
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
In Figure 4, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14)
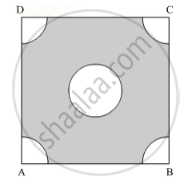
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
