Advertisements
Advertisements
प्रश्न
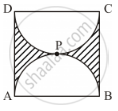
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
उत्तर
The length of the sides of square ABCD is 14 cm.
∴ AB = BC = CD = AD = 14 cm
Radius of each semi-circular portion `14/2 "cm" =7 "cm"`
Perimeter of the shaded region = Perimeter of semi-circle APB + perimeter of semi-circle CPD + BC + AD
`\text{Perimeterof semi - circle APB}=1/2xx2pixxradius=1/2xx2pixx7 cm =22/7 xx7cm =22cm`
`\text{Perimeterof semi - circle CPD}=1/2xx2pixxradius=1/2xx2pixx7 cm =22/7 xx7cm =22cm`
∴ Perimeter of the shaded region = 22 cm + 22 cm + 14 cm + 14 cm = 72 cm
APPEARS IN
संबंधित प्रश्न
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
If the area of an equilateral triangle is `36sqrt3 cm^2` find its perimeter.
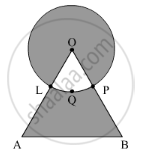
Find the area of shaded region in Fig. 4, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (Use π = 3.14 and\[\sqrt{3}\] =1.73)
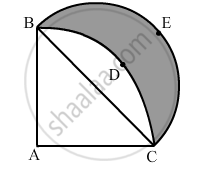
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
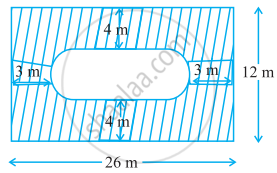
Find the area of the flower bed (with semi-circular ends) shown in figure.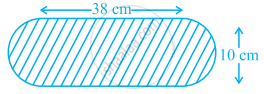
Find the area of the shaded region in figure.