Advertisements
Advertisements
प्रश्न
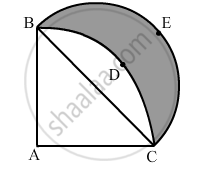
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
उत्तर
Given:
Radius (r) of the circle = AB = AC = 28 cm
Area of quadrant ABDC:
\[= \frac{1}{4} \times \pi \times r^2 \]
\[ = \left( \frac{1}{4} \times \frac{22}{7} \times 28 \times 28 \right) {cm}^2 \]
\[ = 616 {cm}^2\]
Area of ∆ABC:
\[= \frac{1}{2} \times AC \times AB\]
\[ = \left( \frac{1}{2} \times 28 \times 28 \right) {cm}^2 \]
\[ = 392 {cm}^2\]
Area of segment BDC = Area of quadrant ABDC
= 224 cm2 ....(i)
BC2 = BA2 + AC2 (By Pythagoras theorem)
⇒ BC2 = (282 + 282) cm2
⇒ BC2 =\[28 \times 28 \times 2\] cm2
\[= \frac{1}{2} \times \pi \times r^2 \]
\[ = \left( \frac{1}{2} \times \frac{22}{7} \times 14\sqrt{2} \times 14\sqrt{2} \right) {cm}^2 \]
\[ = \left( \frac{1}{2} \times \frac{22}{7} \times 14 \times 14 \times 2 \right) {cm}^2 \]
\[ = 616 {cm}^2\]
Area of the shaded portion = Area of semi-circle BEC −-Area of segment BDC
= 616 cm2 − 224 cm2
= 392 cm2
APPEARS IN
संबंधित प्रश्न
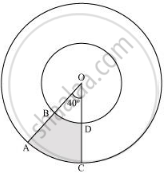
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
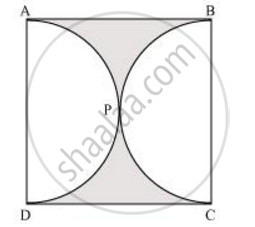
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
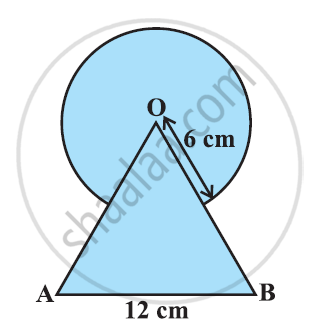
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
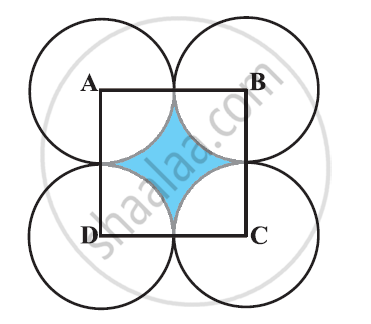
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
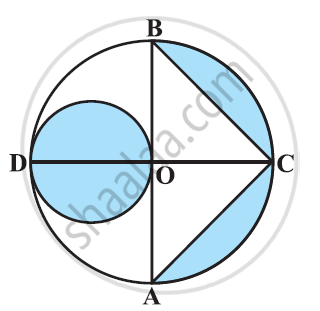
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. [Use Π = 22/7]
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
Find the area of shaded region in Fig. 4, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (Use π = 3.14 and\[\sqrt{3}\] =1.73)
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
