Advertisements
Advertisements
प्रश्न
Find the area of the quadrilateral ABCD, whose vertices are A(−3, −1), B (−2, −4), C(4, − 1) and D (3, 4).
उत्तर
The given quadrilateral i.e., ABCD whose vertices are A (−3, −1), B (−2, −4), C (4, −1) and D (3, 4) can be drawn as follows:
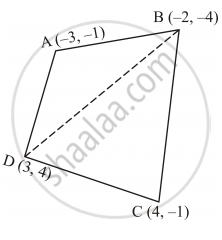
Here, B is joined with D.
We know that the area of a triangle whose vertices are (x1 , y1 ), (x2 , y2 ) and (x3 , y3 ) is given by
`=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`=1/2[-3(-8)-2(5)+3(3)]`
`=1/2[24-10+9]`
`=23/2`
`=11.5 sq.inits`
∴ar(ΔABD)
`=1/2[-3(-4-4)+(-2)(4+1)+3(-1+4)]`
∴ar (ΔCDB)
`=1/2[4(4+4)+3(-4+1)+(-2)(-1-4)]`
`=1/2[(4xx8)+(3x-3)-2xx(-5)]`
`=1/2[32-9+10]`
`=33/2`
`=16.5 sp.unit`
Thus, ar (ABCD) = ar (ΔABD) + ar (ΔCDB) = (11.5 + 16.5) sq units = 28 sq units
APPEARS IN
संबंधित प्रश्न
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle.
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
Name the quadrilateral formed, if any, by the following points, and given reasons for your answers:
A(-3, 5) B(3, 1), C (0, 3), D(-1, -4)
The line segment joining the points P(3, 3) and Q(6, -6) is trisected at the points A and B such that Ais nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k.
Determine the ratio in which the point (-6, a) divides the join of A (-3, 1) and B (-8, 9). Also, find the value of a.
The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0. Find the value of k.
Show that the following points are the vertices of a rectangle
A (0,-4), B(6,2), C(3,5) and D(-3,-1)
Find the area of quadrilateral ABCD whose vertices are A(-5, 7), B(-4, -5) C(-1,-6) and D(4,5)
Find the ratio in which the point (−3, k) divides the line-segment joining the points (−5, −4) and (−2, 3). Also find the value of k ?
Show that `square` ABCD formed by the vertices A(-4,-7), B(-1,2), C(8,5) and D(5,-4) is a rhombus.
Points (−4, 0) and (7, 0) lie
The ordinate of any point on x-axis is
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles.
If the point P (m, 3) lies on the line segment joining the points \[A\left( - \frac{2}{5}, 6 \right)\] and B (2, 8), find the value of m.
If the area of the triangle formed by the points (x, 2x), (−2, 6) and (3, 1) is 5 square units , then x =
If P(2, 4), Q(0, 3), R(3, 6) and S(5, y) are the vertices of a parallelogram PQRS, then the value of y is
If the points P(1, 2), Q(0, 0) and R(x, y) are collinear, then find the relation between x and y.
Given points are P(1, 2), Q(0, 0) and R(x, y).
The given points are collinear, so the area of the triangle formed by them is `square`.
∴ `1/2 |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = square`
`1/2 |1(square) + 0(square) + x(square)| = square`
`square + square + square` = 0
`square + square` = 0
`square = square`
Hence, the relation between x and y is `square`.
The distance of the point (–6, 8) from x-axis is ______.
Assertion (A): The point (0, 4) lies on y-axis.
Reason (R): The x-coordinate of a point on y-axis is zero.
Distance of the point (6, 5) from the y-axis is ______.
