Advertisements
Advertisements
प्रश्न
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
उत्तर
Let the sides of the triangular field be 25x, 17x and 12x. As, perimeter = 540 m
⇒ `25x+17x+12x=540`
⇒` 54x=540`
⇒`x=540/54`
⇒`x=10`
So, the sides are 250 m, 170 m and 120 m.
Now, semi-perimeter, `s= (250+170+120)/2=540/2=270m`
So, area of the filed= `sqrt(270(270-250)(270-170)(270-120))`
=`sqrt(270xx20xx100xx150)`
=`sqrt(3^2xx10xx2xx10xx10^2xx3xx5xx10)`
=`3^2xx10^3`
=`9000m^2`
Also, the cost of ploughing the field=`(9000xx40)/100=3600`
APPEARS IN
संबंधित प्रश्न
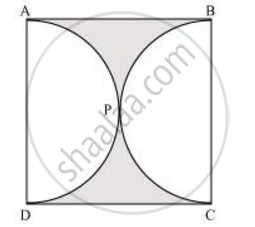
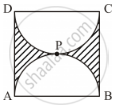
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
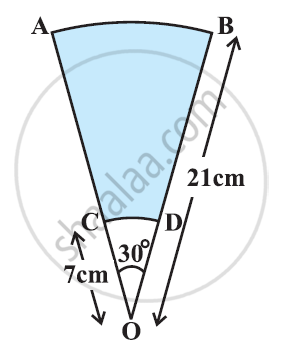
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
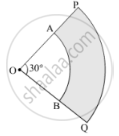
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
If the area of an equilateral triangle is `81sqrt3 cm^2` find its height.
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
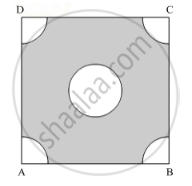
In Figure 4, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14)
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
Find the area of the shaded region in figure.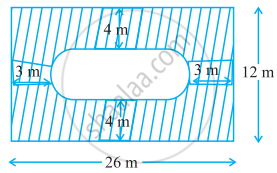
Read the following passage:
Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a hill, which will have adequate space for parking.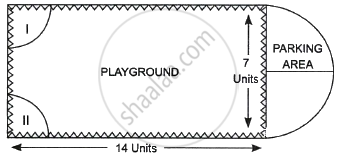 After survey, it was decided to build rectangular playground, with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and 7 units, respectively. There are two quadrants of radius 2 units on one side for special seats. |
Based on the above information, answer the following questions:
- What is the total perimeter of the parking area?
- (a) What is the total area of parking and the two quadrants?
OR
(b) What is the ratio of area of playground to the area of parking area? - Find the cost of fencing the playground and parking area at the rate of ₹ 2 per unit.
