Advertisements
Advertisements
प्रश्न
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
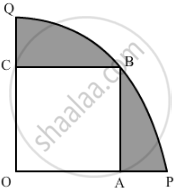
उत्तर
Let us join OB.
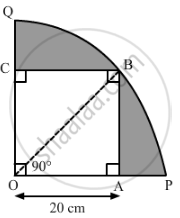
In ΔOAB:
OB2 = OA2 + AB2 = (20)2 + (20)2 = 2 × (20)2
⇒ OB = 20 √2
Radius of the circle, r = `20 sqrt2` cm
`"Area of qudrant OBPQ"=90^@/360^@xx3.14xx(20sqrt2)^2`
`=90/360xx3.14xx(20sqrt2)^2 cm^2`
`=1/4xx3.14xx800 cm^2`
`=628 cm^2`
Area of square OABC = (Side)2 = (20)2 cm2 = 400 cm2
∴ Area of the shaded region = Area of quadrant OPBQ − Area of square OA
= (628 − 400) cm2
= 228 cm2
APPEARS IN
संबंधित प्रश्न
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
