Advertisements
Advertisements
प्रश्न
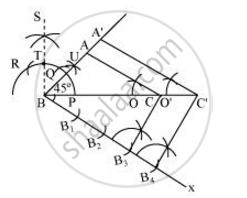
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are `4/3 `times the corresponding side of ΔABC. Give the justification of the construction.
उत्तर
∠B = 45°, ∠A = 105°
Sum of all interior angles in a triangle is 180°.
∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C = 180° − 150°
∠C = 30°
The required triangle can be drawn as follows.
Step 1
Draw a ΔABC with side BC = 7 cm, ∠B = 45°, ∠C = 30°.
Step 2
Draw a ray BX making an acute angle with BC on the opposite side of vertex A.
Step 3
Locate 4 points (as 4 is greater in 4 and 3), B1, B2, B3, B4, on BX.
Step 4
Join B3C. Draw a line through B4 parallel to B3C intersecting extended BC at C'.
Step 5
Through C', draw a line parallel to AC intersecting extended line segment at C'. ΔA'BC' is the required triangle.
Justification
The construction can be justified by proving that
`A'B = 4/3 AB, BC' = 4/3BC , A'C' = 4/3 AC`
n ΔABC and ΔA'BC',
∠ABC = ∠A'BC' (Common)
∠ACB = ∠A'C'B (Corresponding angles)
∴ ΔABC ∼ ΔA'BC' (AA similarity criterion)
`=>(AB)/(A'B) = (BC)/(BC') = (AC)/(A'C') ....1`
In ΔBB3C and ΔBB4C',
∠B3BC = ∠B4BC' (Common)
∠BB3C = ∠BB4C' (Corresponding angles)
∴ ΔBB3C ∼ ΔBB4C' (AA similarity criterion)
`=>(BC)/(BC') = `
`=>(BC)/(BC') = 3/4 ...(2)`
On comparing equations (1) and (2), we obtain
`(AB)/(A'B) = (BC)/(BC')=(AC)/(A'C') = 3/4`
`=> A'B = 4/3 AB, BC' = 4/3 BC, A'C' = 4/3 AC`
This justifies the construction.
APPEARS IN
संबंधित प्रश्न
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose side are `1 1/2` times the corresponding sides of the isosceles triangle.
Give the justification of the construction
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. the construct another triangle whose sides are `5/3` times the corresponding sides of the given triangle. Give the justification of the construction.
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)th of the corresponding sides of ΔABC.
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\] of the corresponding sides of ∆ABC ?
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are `2/3` times the corresponding sides of ΔABC.
The line segment AB is divided into five congruent parts at P, Q, R and S such that A–P–Q–R–S–B. If point Q(12, 14) and S(4, 18) are given find the coordinates of A, P, R, B.
∆ABC ~ ∆PBQ. In ∆ABC, AB = 3 cm, ∠B = 90°, BC = 4 cm. Ratio of the corresponding sides of two triangles is 7 : 4. Then construct ∆ABC and ∆PBQ
By geometrical construction, it is possible to divide a line segment in the ratio `sqrt(3) : 1/sqrt(3)`.
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
