Advertisements
Advertisements
प्रश्न
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)th of the corresponding sides of ΔABC.
उत्तर
Given that
Construct a triangle of sides BC = 6 cm, AB = 4 cm and AC = 5 cm and then a triangle similar to it whose sides are (3/4)th of the corresponding sides of ΔABC.
We follow the following steps to construct the given
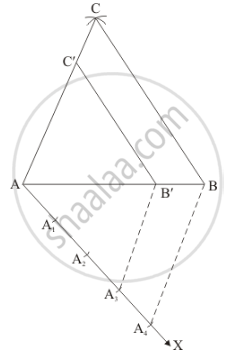
Step of construction
Step: I- First of all we draw a line segment AB = 4 cm.
Step: II- With A as centre and radius = AC = 5 cm, draw an arc.
Step: III -With B as centre and radius = BC = 6 cm, draw an arc, intersecting the arc drawn in step II at C.
Step: IV -Joins AC and BC to obtain ΔABC.
Step: V -Below AB, makes an acute angle ∠BAX = 60°.
Step: VI -Along AX, mark off four points A1, A2, A3 and A4 such that AA1 = A1A2 = A2A3 = A3A4
Step: VII -Join A4B.
Step: VIII -Since we have to construct a triangle each of whose sides is (3/4)th of the corresponding sides of ΔABC.
So, we take three parts out of four equal parts on AX from point A3 draw A3B' || A4B, and meeting AB at B’.
Step: IX- From B’ draw B'C || BC and meeting AC at C’
Thus, ΔAB'C' is the required triangle, each of whose sides is (3/4)th of the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60˚. Now construct another triangle whose sides are 5/7 times the corresponding sides of ΔABC.
If A (20, 10), B(0, 20) are given, find the coordinates of the points which divide segment AB into five congruent parts.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point on the circle.
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
For ∆ABC in which BC = 7.5cm, ∠B =45° and AB - AC = 4, select the correct figure.
When a line segment is divided in the ratio 2 : 3, how many parts is it divided into?
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
To divide a line segment, the ratio of division must be ______.
To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ...., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.
Draw an isosceles triangle ABC in which AB = AC = 6 cm and BC = 5 cm. Construct a triangle PQR similar to ∆ABC in which PQ = 8 cm. Also justify the construction.
