Advertisements
Advertisements
प्रश्न
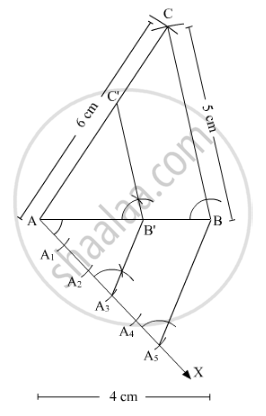
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\] of the corresponding sides of ∆ABC ?
उत्तर
Steps of Construction
Step 1
Draw a line segment AB = 4 cm. Taking point A as the centre and radius 6 cm, draw an arc. Similarly, taking point B as the centre and radius 5 cm, draw another arc. The arcs will intersect at point C. Now, join AC and BC to obtain the required triangle ABC.
Step 2
Draw a ray AX making an acute angle with line AB on the opposite side of vertex C.
Step 3
Locate five points A1, A2, A3, A4 and A5 on line AX such that AA1 = A1A2 = A2A3 = A3A4 = A4A5
Step 4
Join BA5 and draw a line through A3 parallel to BA5 to intersect AB at point B'.
Step 5
Draw a line through B' parallel to line BC to intersect AC at C'.
AB'C' is the required triangle.
APPEARS IN
संबंधित प्रश्न
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. the construct another triangle whose sides are `5/3` times the corresponding sides of the given triangle. Give the justification of the construction.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are `3/5` times the corresponding sides of the given triangle.
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3 Also, justify your construction.
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)th of the corresponding sides of ΔABC.
The line segment AB is divided into five congruent parts at P, Q, R and S such that A–P–Q–R–S–B. If point Q(12, 14) and S(4, 18) are given find the coordinates of A, P, R, B.
Δ SHR ∼ Δ SVU. In Δ SHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and
SHSV = 53 then draw Δ SVU.
Draw seg AB of length 9 cm and divide it in the ratio 3 : 2
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
If you need to construct a triangle with point P as one of its vertices, which is the angle that you need to construct a side of the triangle?
What is the ratio `(AC)/(BC)` for the following construction: A line segment AB is drawn. A single ray is extended from A and 12 arcs of equal lengths are cut, cutting the ray at A1, A2… A12.A line is drawn from A12 to B and a line parallel to A12B is drawn, passing through the point A6 and cutting AB at C.
