Question

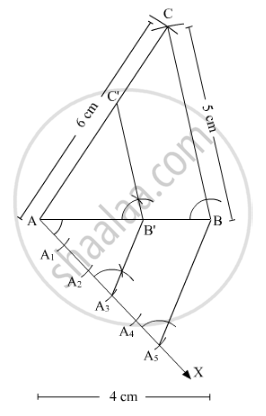
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\]  of the corresponding sides of ∆ABC ?

Answer 1

Steps of Construction

Step 1

Draw a line segment AB = 4 cm. Taking point A as the centre and radius 6 cm, draw an arc. Similarly, taking point B as the centre and radius 5 cm, draw another arc. The arcs will intersect at point C. Now, join AC and BC to obtain the required triangle ABC.

Step 2

Draw a ray AX making an acute angle with line AB on the opposite side of vertex C.

Step 3

Locate five points A₁, A₂, A₃, A₄ and A₅  on line AX such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅

Step 4

Join BA₅ and draw a line through A₃ parallel to BA₅ to intersect AB at point B'.

Step 5

Draw a line through B' parallel to line BC to intersect AC at C'.

AB'C' is the required triangle.