Advertisements
Advertisements
प्रश्न
∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. `"AM"/"AH" = 7/5`. Construct ∆AHE.
∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. `"AM"/"AH" = 7/5`. then construct △AMT and ΔAHE.
Advertisements
उत्तर
Analysis:
|
|
As shown in the figure,
Let A – H – M as well as points A – E – T be collinear.
∆AMT ~ ∆AHE,
∴ ∠TAM ≅ ∠EAH ...(Corresponding angles of similar triangles)
`"AM"/"AH" = "MT"/"HE" = "AT"/"AE"` ...(i)(Corresponding sides of similar triangles)
∴ `"AM"/"AH" = 7/5` ...(ii)(Given)
`"AM"/"AH" = "MT"/"HE" = "AT"/"AE" = 7/5` ...[From (i) and (ii)]
∴ sides of ∆AHE are smaller than sides of ∆AMT.
∴ If seg AH will be equal to 5 parts out of 7 equal parts of side AM.
So, if we construct ∆AMT, point H will be on side AM, at a distance equal to 5 parts from A.
Now, point E is the point of intersection of ray AT and a line through H, parallel to MT.
∆AHE is the required triangle similar to ∆AMT.
Steps of Construction:
- Draw ∆AMT such that AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm.
- Draw ray AB making an acute angle with side AM.
- Taking convenient distance on the compass, mark 7 points A1, A2, A3, A4, A5, A6 and A7, such that AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7.
- Join A7M. Draw line parallel to A7M through A5 to intersects seg AM at H.
- Draw a line parallel to side TM through H. Name the point of intersection of this line and seg AT as E.
∆AHE is the required triangle similar to ∆AMT.
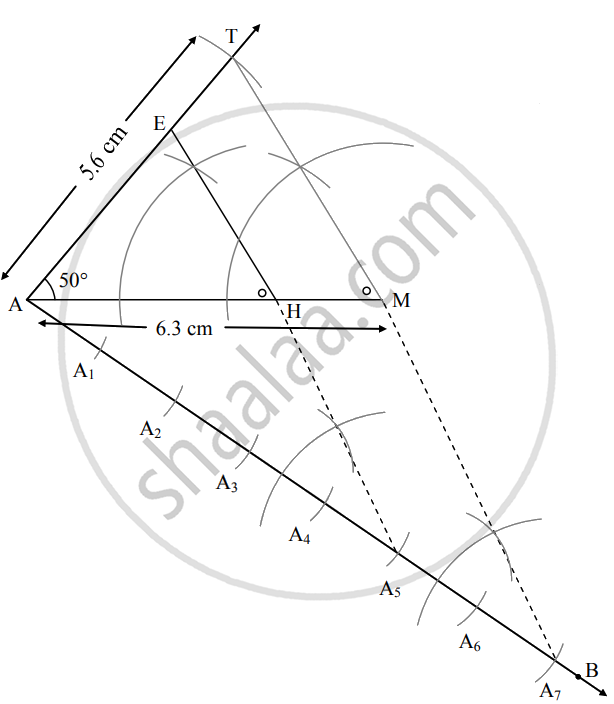
Here, ∆AMT ~ ∆AHE.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are`3/4` times the corresponding sides of ΔABC.
Construct a triangle ABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts. Give the justification of the construction.
Construct a triangle of sides 4 cm, 5cm and 6cm and then a triangle similar to it whose sides are `2/3` of the corresponding sides of the first triangle. Give the justification of the construction.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. the construct another triangle whose sides are `5/3` times the corresponding sides of the given triangle. Give the justification of the construction.
Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5
Draw a line segment of length 7 cm and divide it internally in the ratio 2 : 3.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are `3/5` times the corresponding sides of the given triangle.
Construct a triangle similar to a given ΔABC such that each of its sides is (2/3)rd of the corresponding sides of ΔABC. It is given that BC = 6 cm, ∠B = 50° and ∠C = 60°.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3th times the corresponding sides of the given triangle.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Find the co-ordinates of the points of trisection of the line segment AB with A(2, 7) and B(–4, –8).
If A (20, 10), B(0, 20) are given, find the coordinates of the points which divide segment AB into five congruent parts.
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
Choose the correct alternative:
In the figure ΔABC ~ ΔADE then the ratio of their corresponding sides is ______
ΔAMT ~ ΔAHE. In ΔAMT, AM = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `"AM"/"HA" = 7/5`, then construct ΔAMT and ΔAHE
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is ______.
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3, .... are located at equal distances on the ray AX and the point B is joined to ______.
To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A1, A2, A3, ... and B1, B2, B3, ... are located at equal distances on ray AX and BY, respectively. Then the points joined are ______.
To construct a triangle similar to a given ΔABC with its sides `3/7` of the corresponding sides of ΔABC, first draw a ray BX such that ∠CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points B1, B2, B3, ... on BX at equal distances and next step is to join ______.
To divide a line segment PQ in the ratio 5 : 7, first a ray PX is drawn so that ∠QPX is an acute angle and then at equal distances points are marked on the ray PX such that the minimum number of these points is ______.
Match the following based on the construction of similar triangles, if scale factor `(m/n)` is.
| Column I | Column II | ||
| i | >1 | a) | The similar triangle is smaller than the original triangle. |
| ii | <1 | b) | The two triangles are congruent triangles. |
| iii | =1 | c) | The similar triangle is larger than the original triangle. |
The image of construction of A’C’B a similar triangle of ΔACB is given below. Then choose the correct option.
To divide a line segment, the ratio of division must be ______.
To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ...., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Draw a right triangle ABC in which BC = 12 cm, AB = 5 cm and ∠B = 90°. Construct a triangle similar to it and of scale factor `2/3`. Is the new triangle also a right triangle?
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Construct a triangle similar to ∆ABC with scale factor `5/7`. Justify the construction.
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
