Advertisements
Advertisements
प्रश्न
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
Advertisements
उत्तर
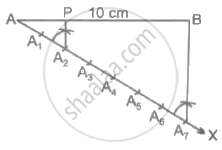
Steps of construction:
- Draw a line segment AB of length 10 cm.
- Draw a line AX making an acute angle with AB.
- Mark 7 points A1, A2, A3, ...... A7 along AX such that AA1 = A1A2 = A1A3 = ...... = A6A7.
- Join point B with point A7.
- Through the point A2, draw a line parallel to A7B by making an angle equal to ∠AA7B at A2. This line meets AB at a point P.
As a result, point P is necessary to divide line AB internally in the ratio of 2 : 5.
Justification: In ΔAA7B, A2P || A7B.
As a result of the basic proportionality theorem,
`(A A_2)/(A_2A_7) = (AP)/(PB)` .......(i)
By the above construction,
`(A A_2)/(A_2A_7) = 2/5` ......(ii)
By equations (i) and (ii),
`(AP)/(PB) = 2/5`
Thus, AP : PB = 2 : 5
As a result, P splits the line AB in the ratio 2 : 5.
APPEARS IN
संबंधित प्रश्न
Write down the equation of a line whose slope is 3/2 and which passes through point P, where P divides the line segment AB joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Construct the circumcircle and incircle of an equilateral triangle ABC with side 6 cm and centre O. Find the ratio of radii of circumcircle and incircle.
Find the ratio in which the line segment joining the points A(3,- 3) and B(- 2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are`4/5` times the corresponding sides of ΔABC.
Construct a triangle ABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Construct a triangle of sides 4 cm, 5cm and 6cm and then a triangle similar to it whose sides are `2/3` of the corresponding sides of the first triangle. Give the justification of the construction.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are `4/3 `times the corresponding side of ΔABC. Give the justification of the construction.
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also, justify your construction.
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)th of the corresponding sides of ΔABC.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
Construct a triangle similar to a given ΔXYZ with its sides equal to (3/4)th of the corresponding sides of ΔXYZ. Write the steps of construction.
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
∆PQR ~ ∆LTR. In ∆PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct ∆PQR and ∆LTR, such that `"PQ"/"LT" = 3/4`.
Construct ∆PYQ such that, PY = 6.3 cm, YQ = 7.2 cm, PQ = 5.8 cm. If \[\frac{YZ}{YQ} = \frac{6}{5},\] then construct ∆XYZ similar to ∆PYQ.
Find the ratio in which point P(k, 7) divides the segment joining A(8, 9) and B(1, 2). Also find k.
Find the co-ordinates of the points of trisection of the line segment AB with A(2, 7) and B(–4, –8).
If A(–14, –10), B(6, –2) is given, find the coordinates of the points which divide segment AB into four equal parts.
The line segment AB is divided into five congruent parts at P, Q, R and S such that A–P–Q–R–S–B. If point Q(12, 14) and S(4, 18) are given find the coordinates of A, P, R, B.
Δ SHR ∼ Δ SVU. In Δ SHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and
SHSV = 53 then draw Δ SVU.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point on the circle.
Choose the correct alternative:
∆ABC ∼ ∆AQR. `"AB"/"AQ" = 7/5`, then which of the following option is true?
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A1, A2, A3, ... and B1, B2, B3, ... are located at equal distances on ray AX and BY, respectively. Then the points joined are ______.
A rhombus ABCD in which AB = 4cm and ABC = 60o, divides it into two triangles say, ABC and ADC. Construct the triangle AB’C’ similar to triangle ABC with scale factor `2/3`. Select the correct figure.
The ratio of corresponding sides for the pair of triangles whose construction is given as follows: Triangle ABC of dimensions AB = 4cm, BC = 5 cm and ∠B= 60°.A ray BX is drawn from B making an acute angle with AB.5 points B1, B2, B3, B4 and B5 are located on the ray such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
B4 is joined to A and a line parallel to B4A is drawn through B5 to intersect the extended line AB at A’.
Another line is drawn through A’ parallel to AC, intersecting the extended line BC at C’. Find the ratio of the corresponding sides of ΔABC and ΔA′BC′.
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
If you need to construct a triangle with point P as one of its vertices, which is the angle that you need to construct a side of the triangle?
The image of construction of A’C’B a similar triangle of ΔACB is given below. Then choose the correct option.
What is the ratio `(AC)/(BC)` for the following construction: A line segment AB is drawn. A single ray is extended from A and 12 arcs of equal lengths are cut, cutting the ray at A1, A2… A12.A line is drawn from A12 to B and a line parallel to A12B is drawn, passing through the point A6 and cutting AB at C.
To divide a line segment, the ratio of division must be ______.
By geometrical construction, it is possible to divide a line segment in the ratio `sqrt(3) : 1/sqrt(3)`.
Draw a right triangle ABC in which BC = 12 cm, AB = 5 cm and ∠B = 90°. Construct a triangle similar to it and of scale factor `2/3`. Is the new triangle also a right triangle?
Draw a triangle ABC in which BC = 6 cm, CA = 5 cm and AB = 4 cm. Construct a triangle similar to it and of scale factor `5/3`.
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
